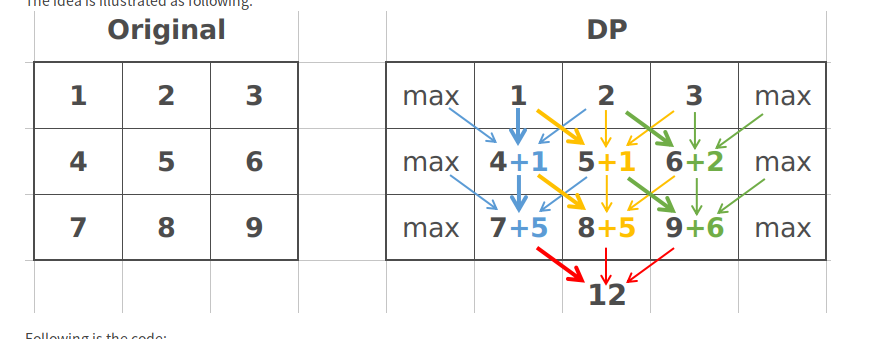
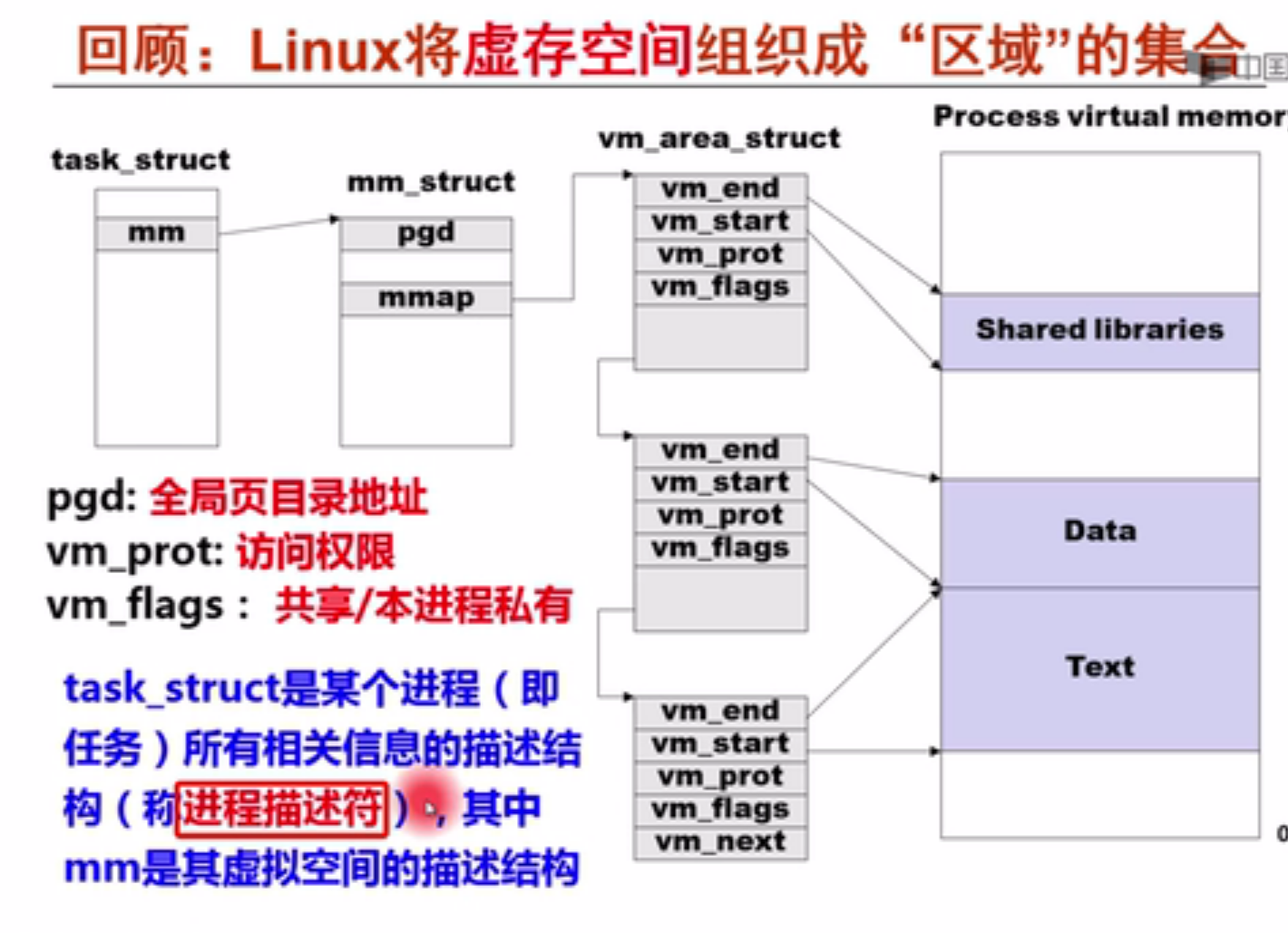
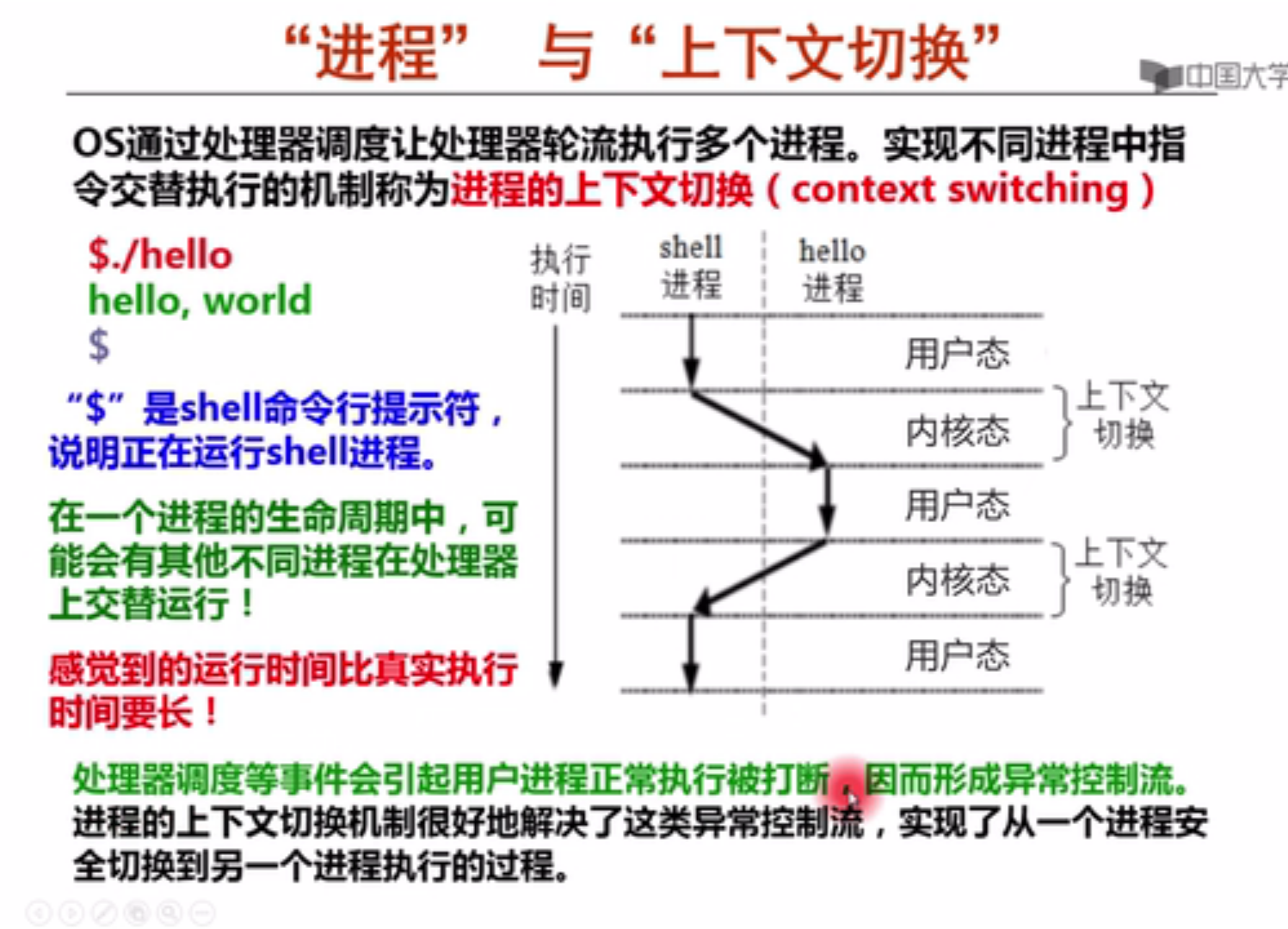
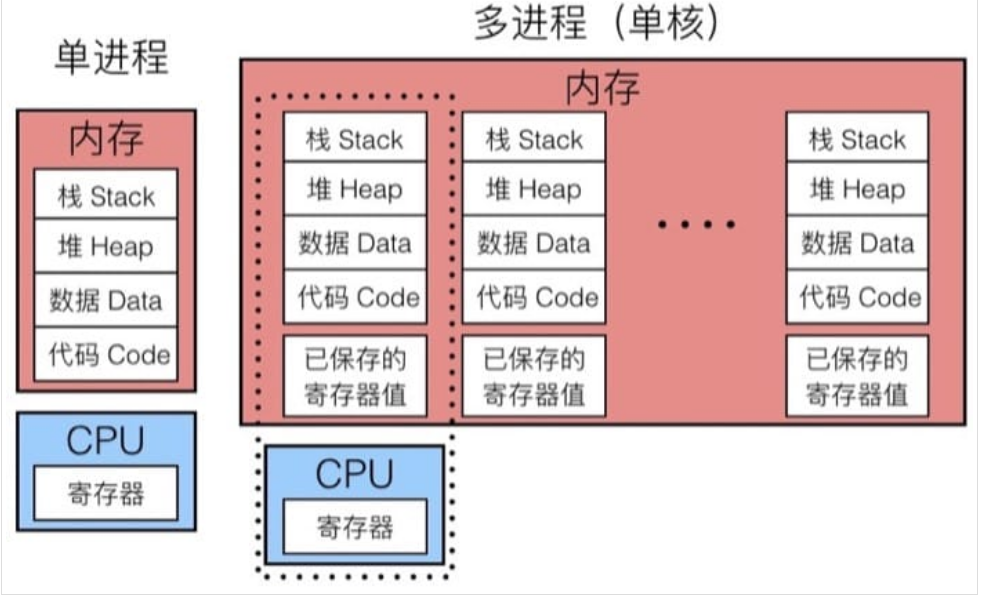
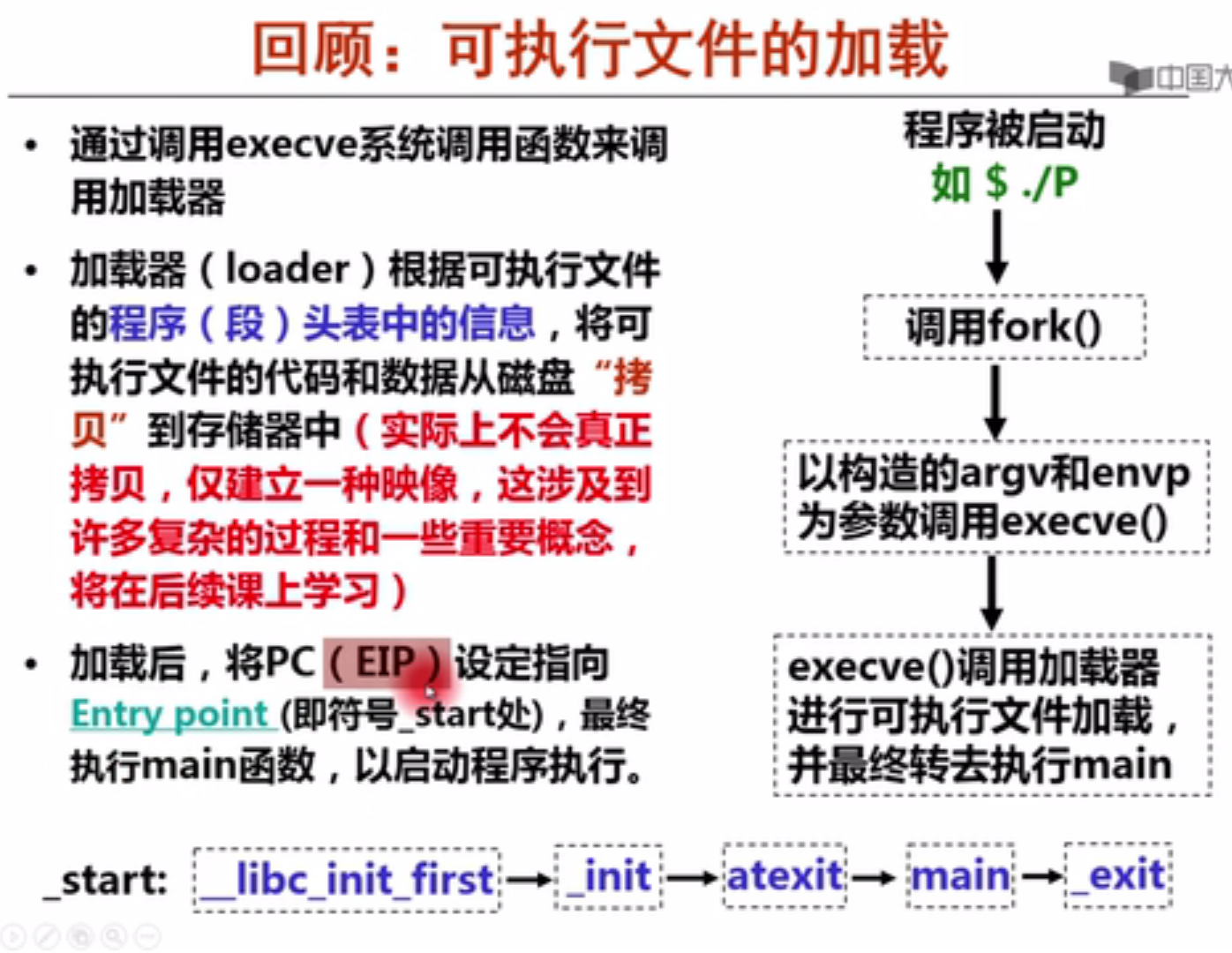
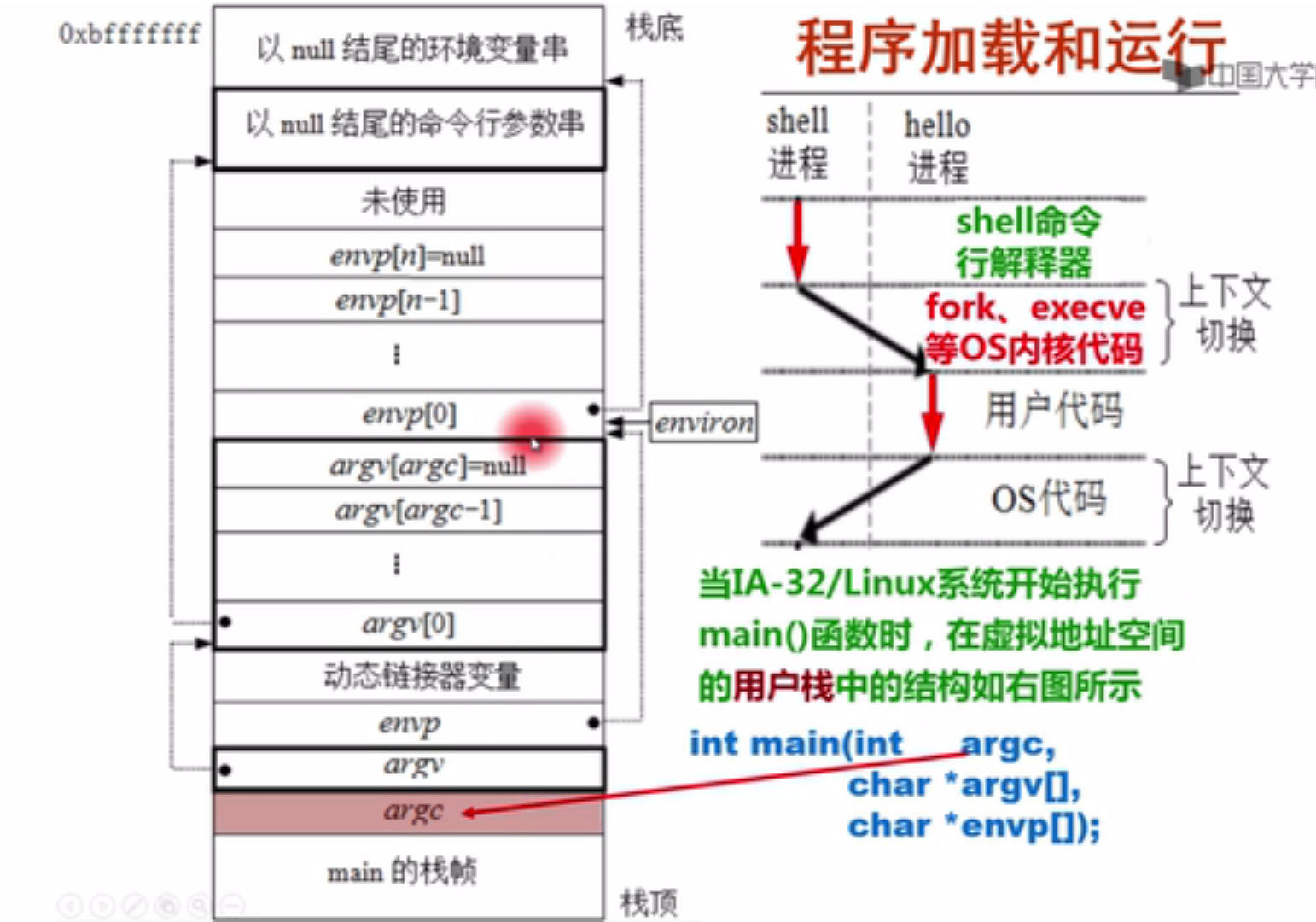
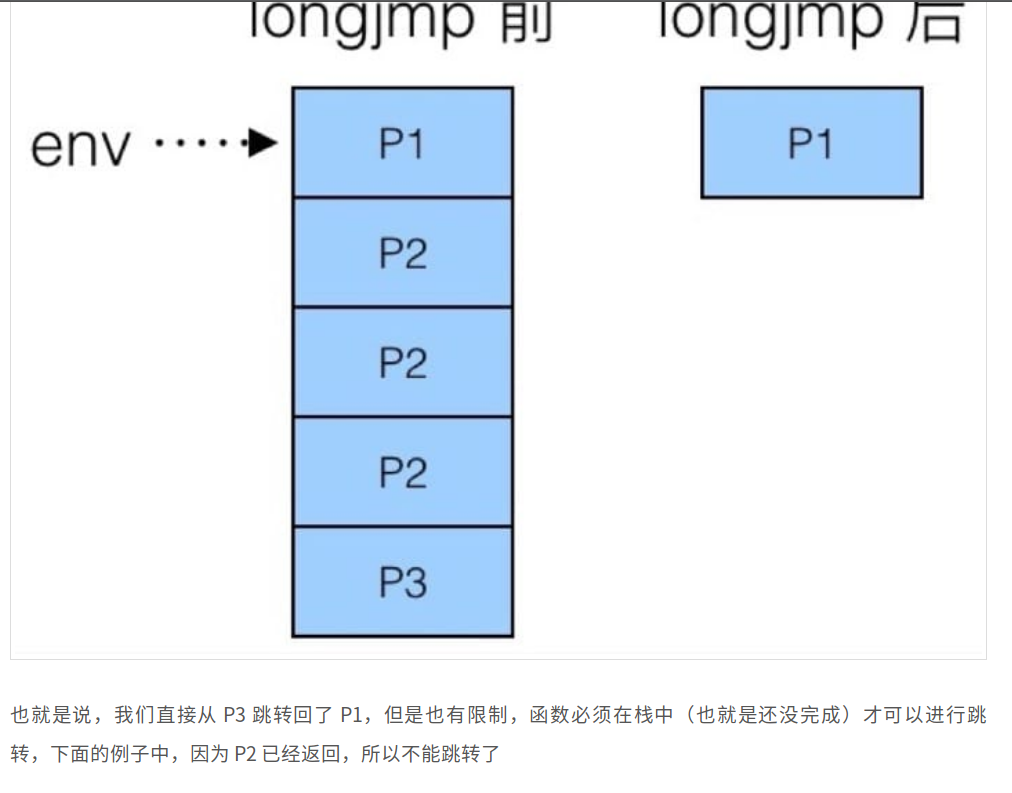
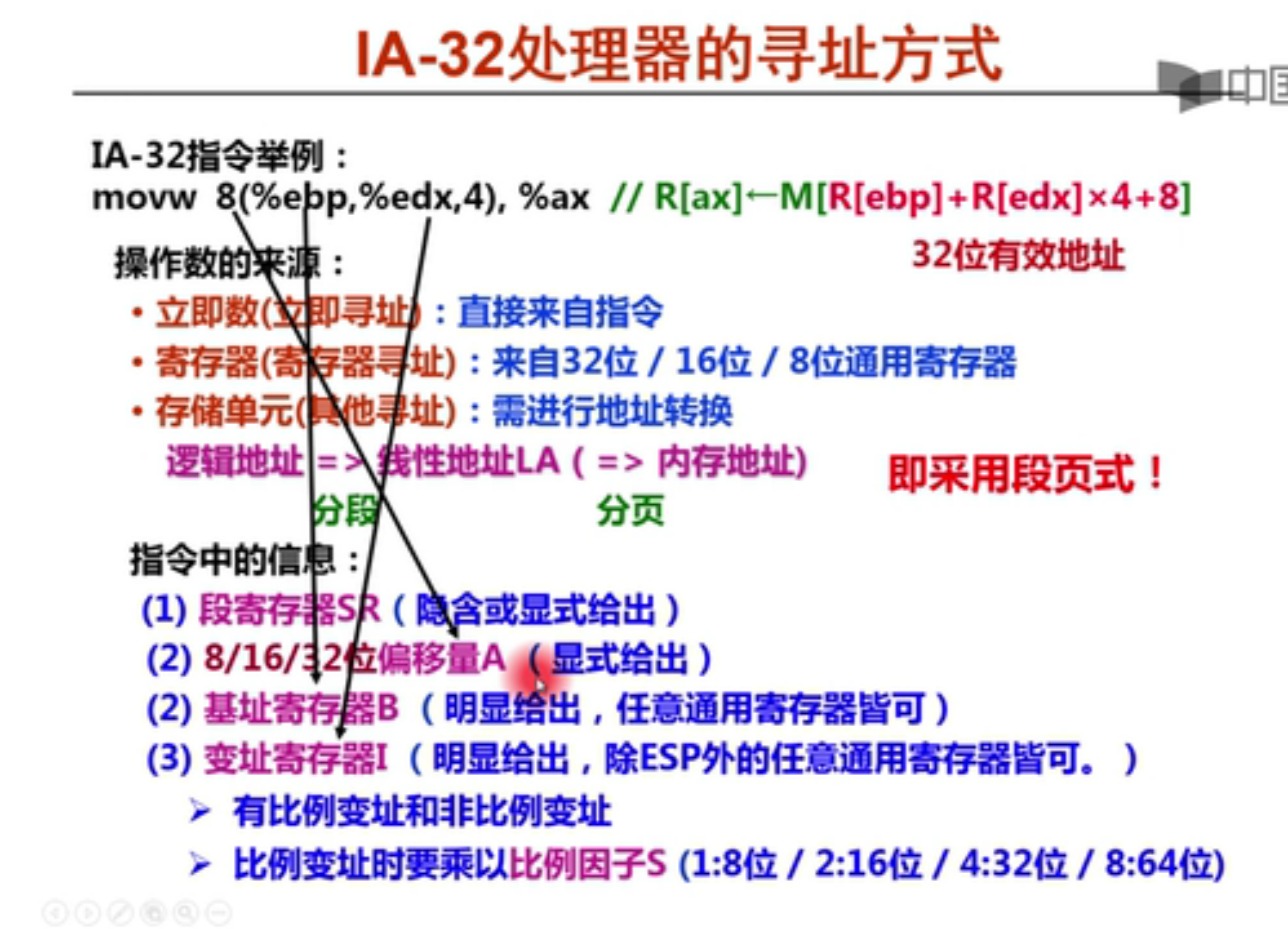
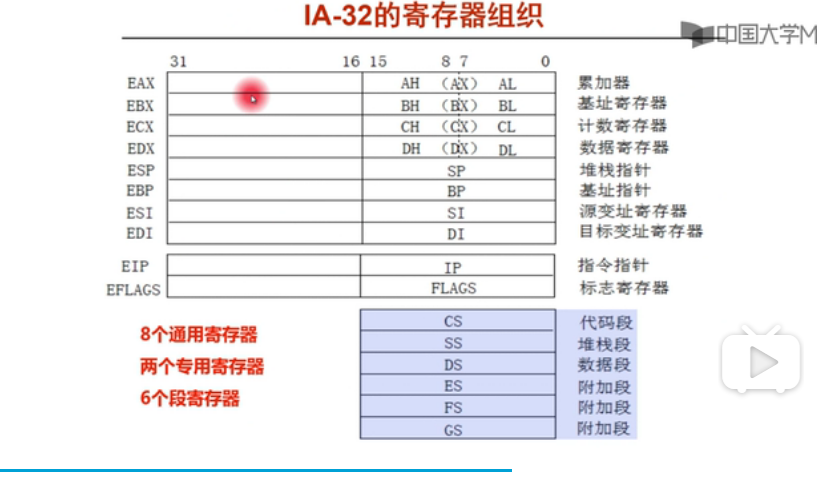
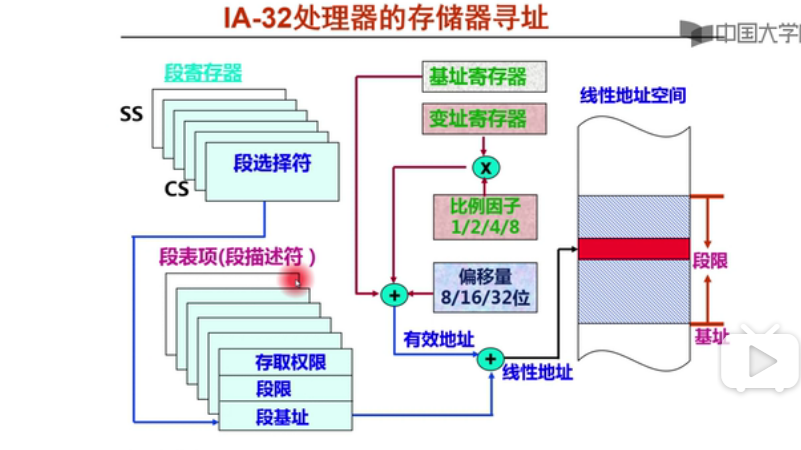
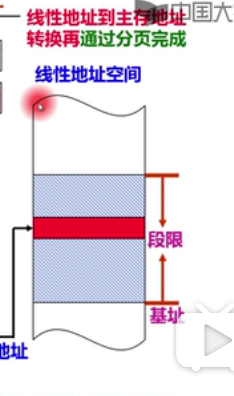
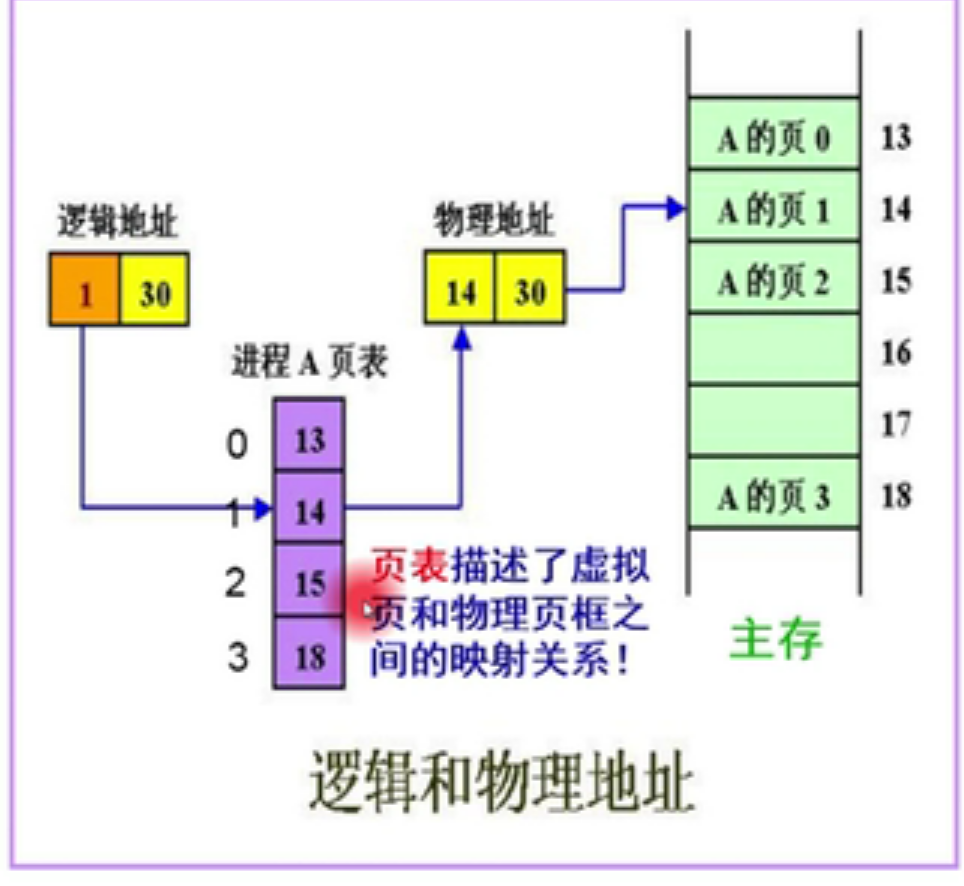
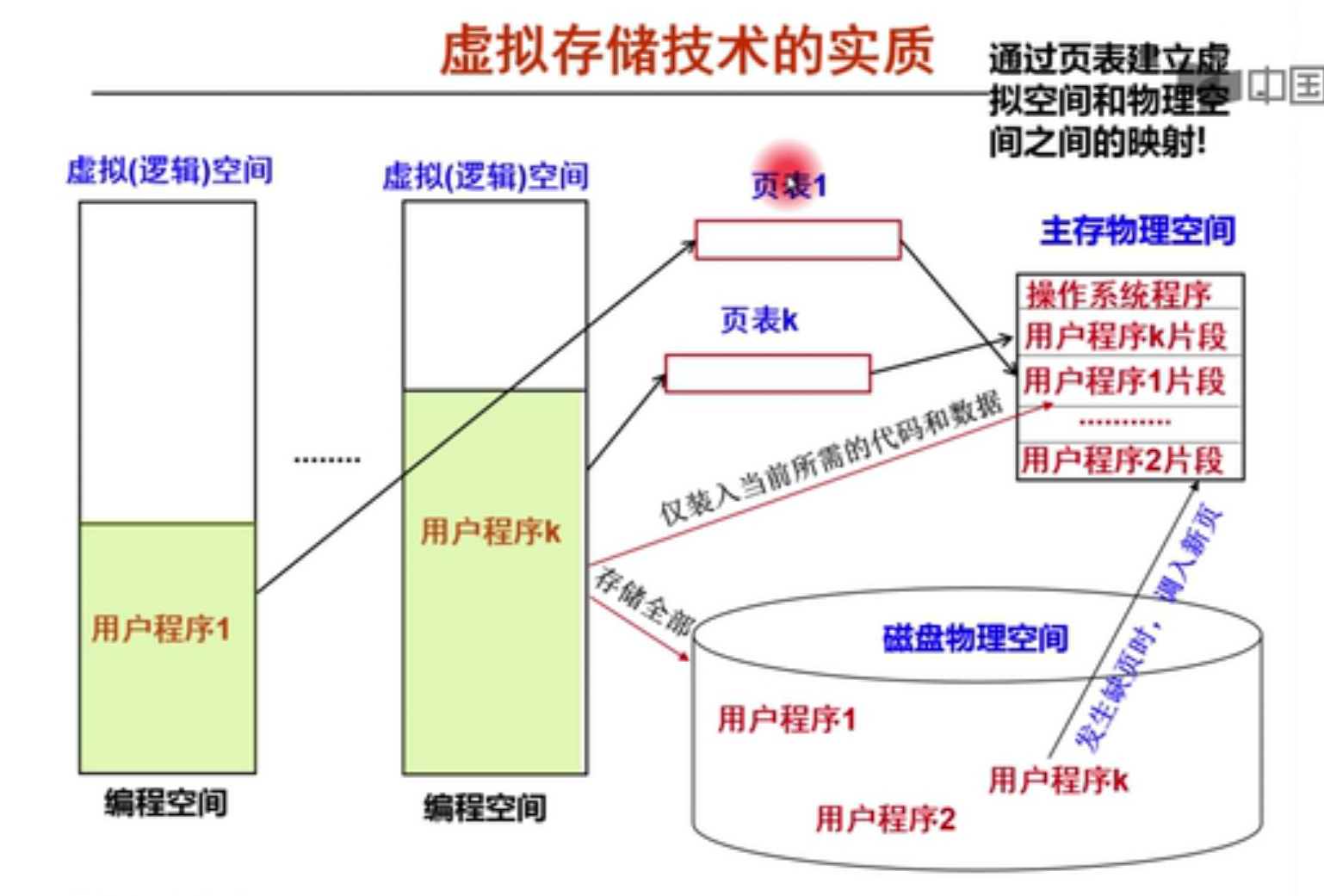
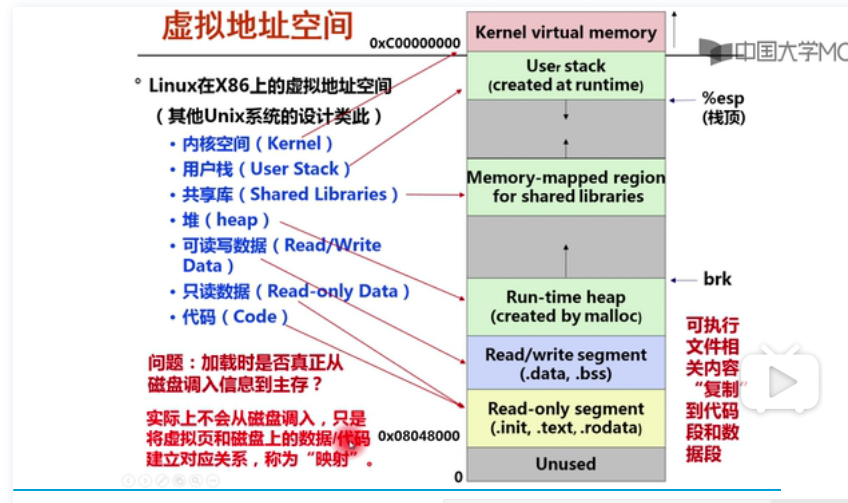
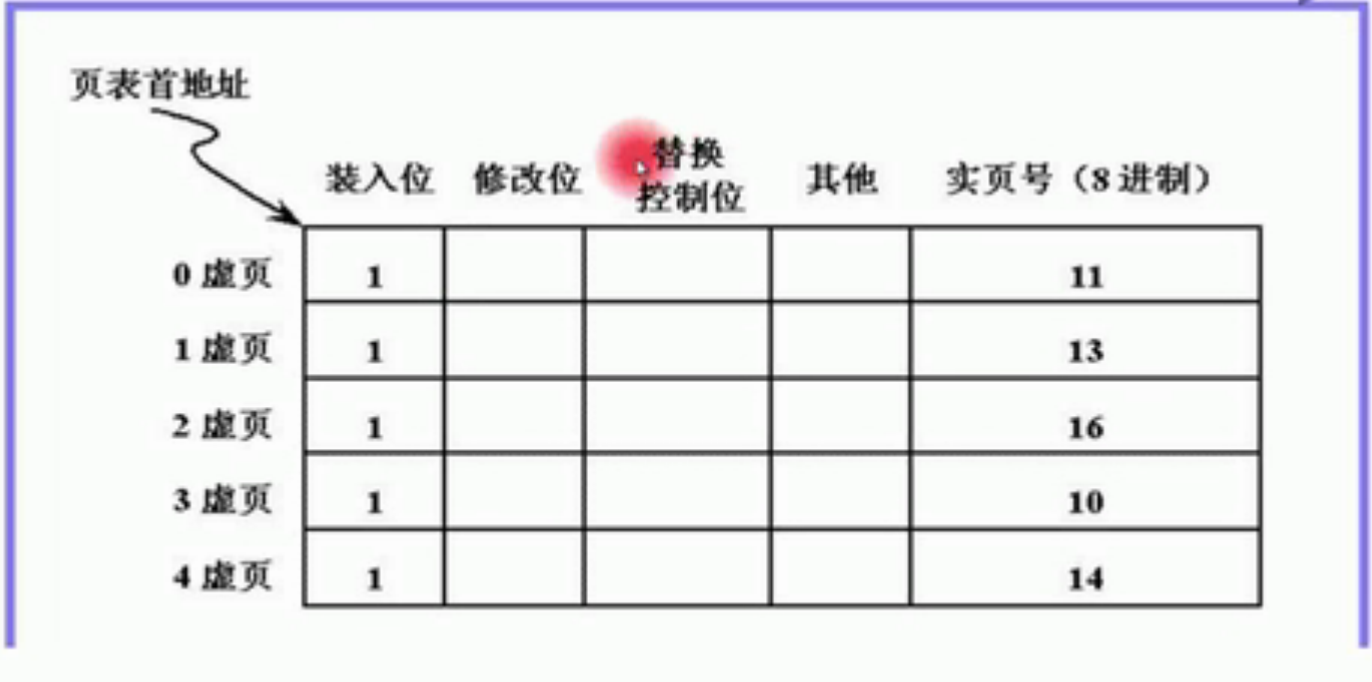
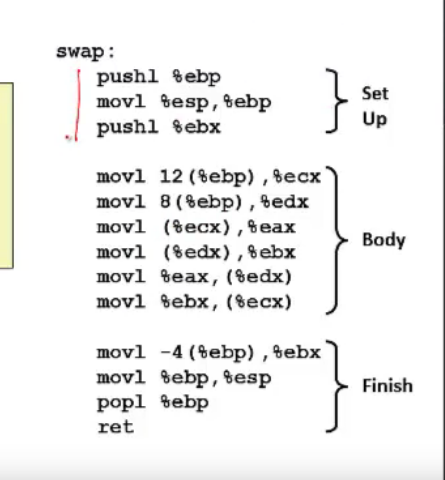
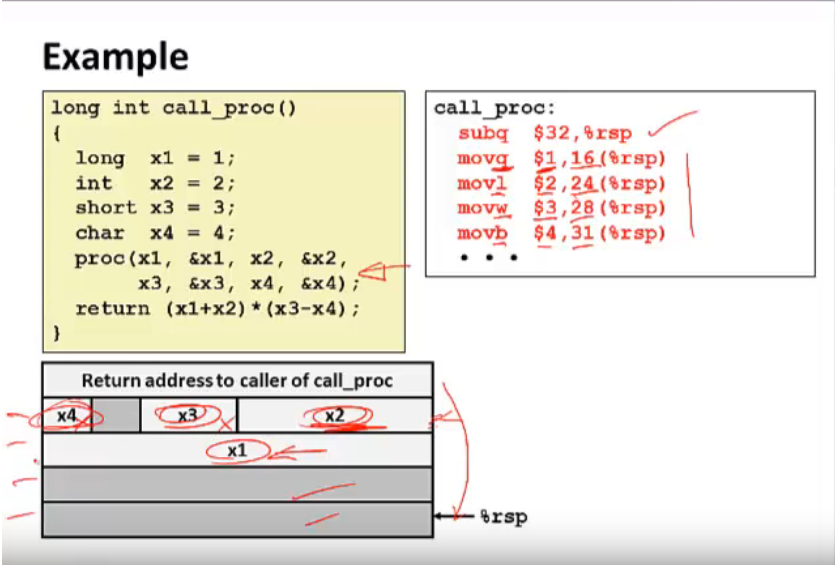
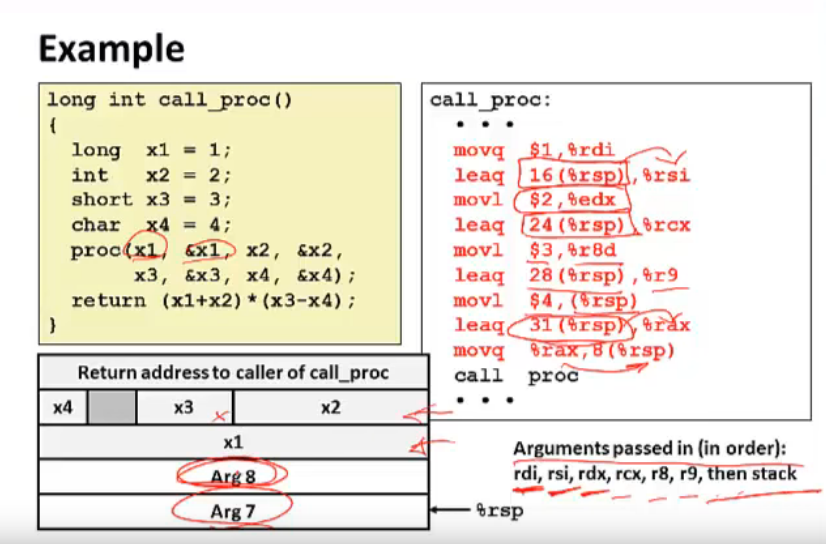
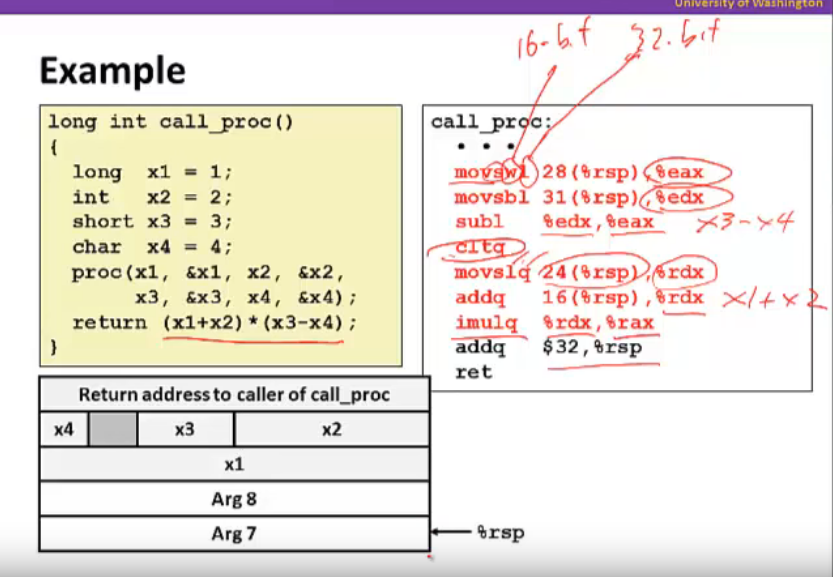
实现思路
所用策略:Segregated lists + best fits + explicit free list
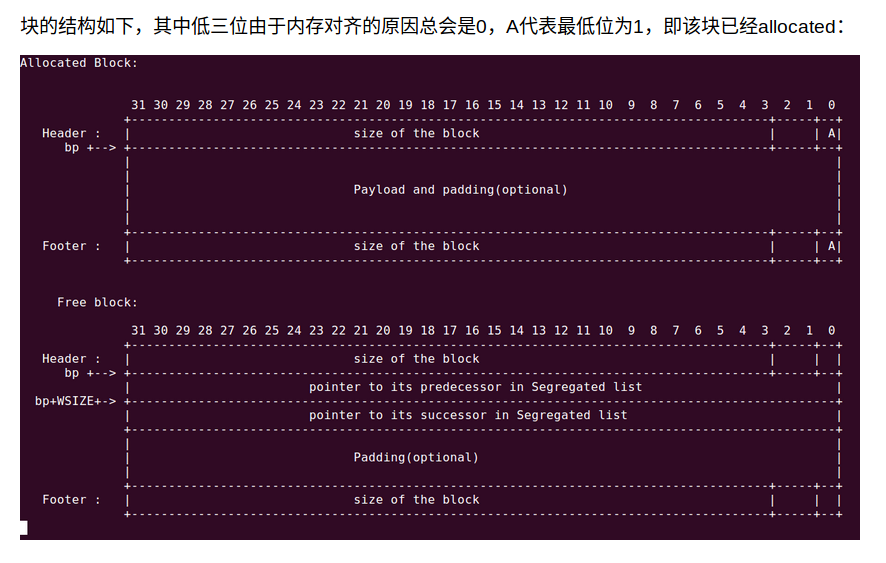
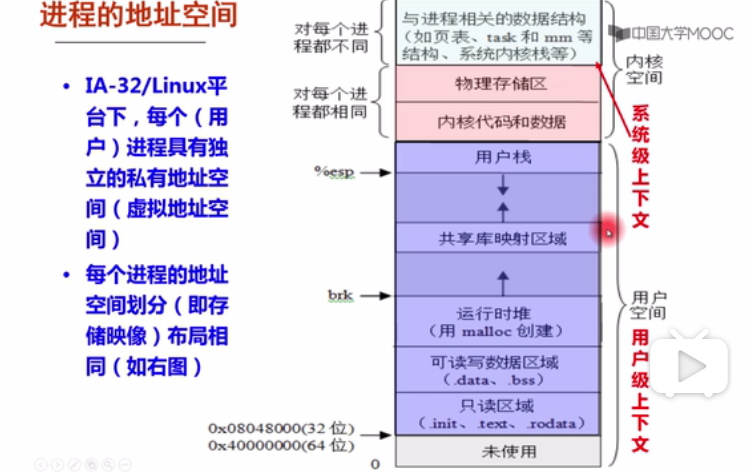
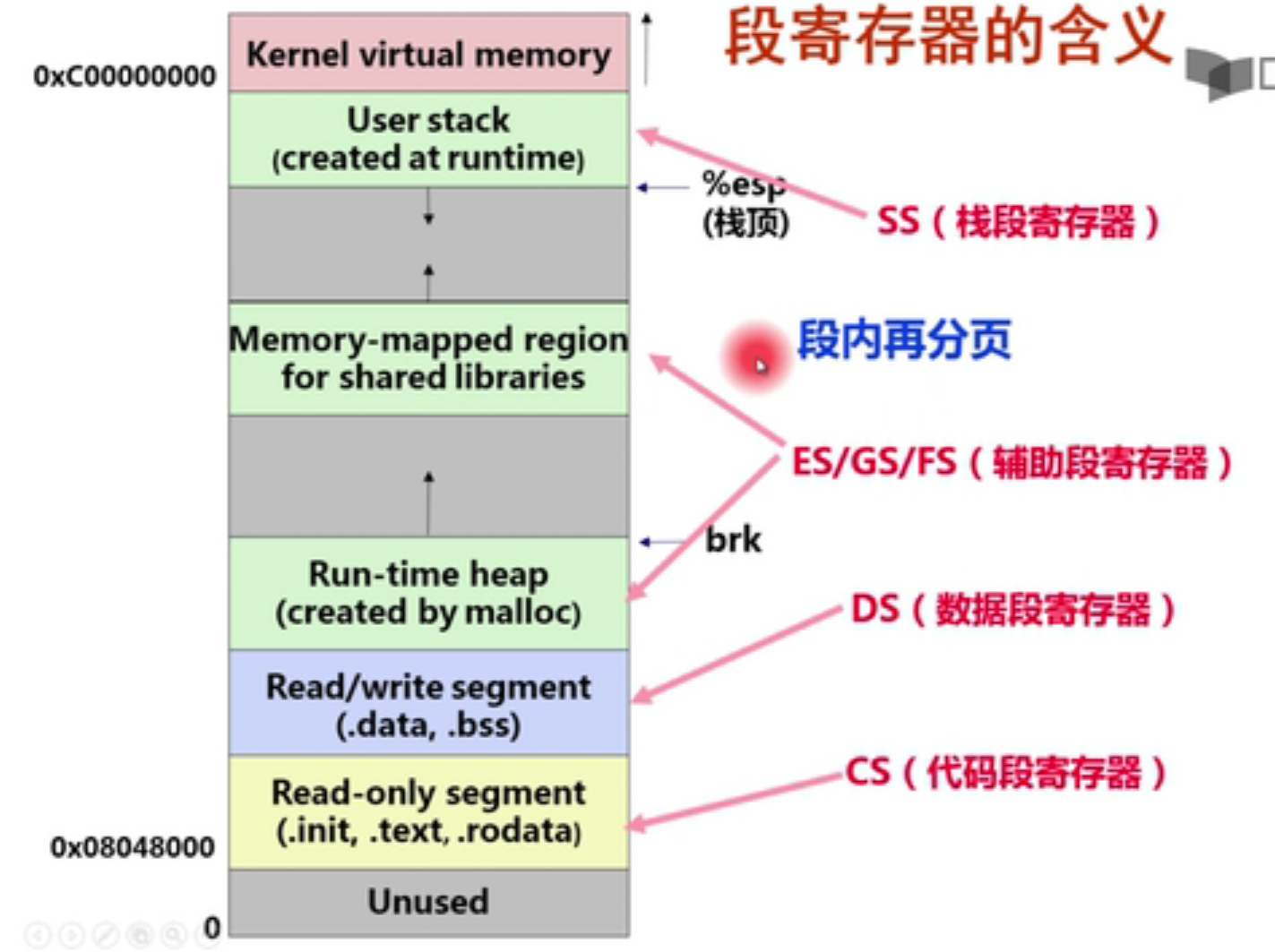
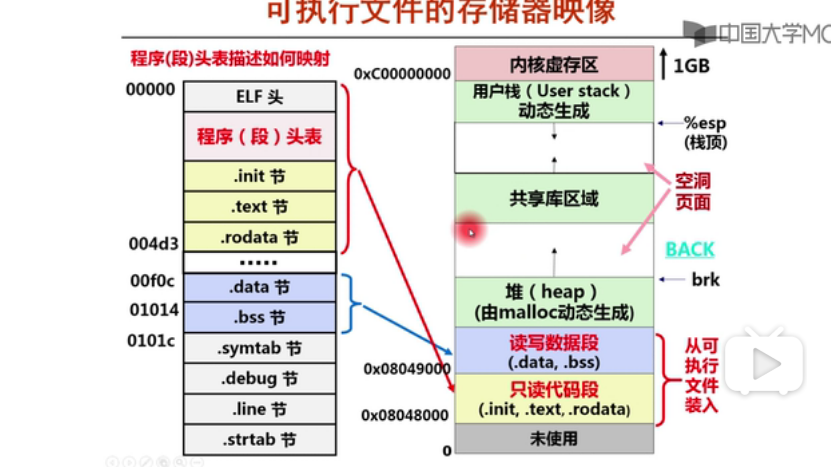
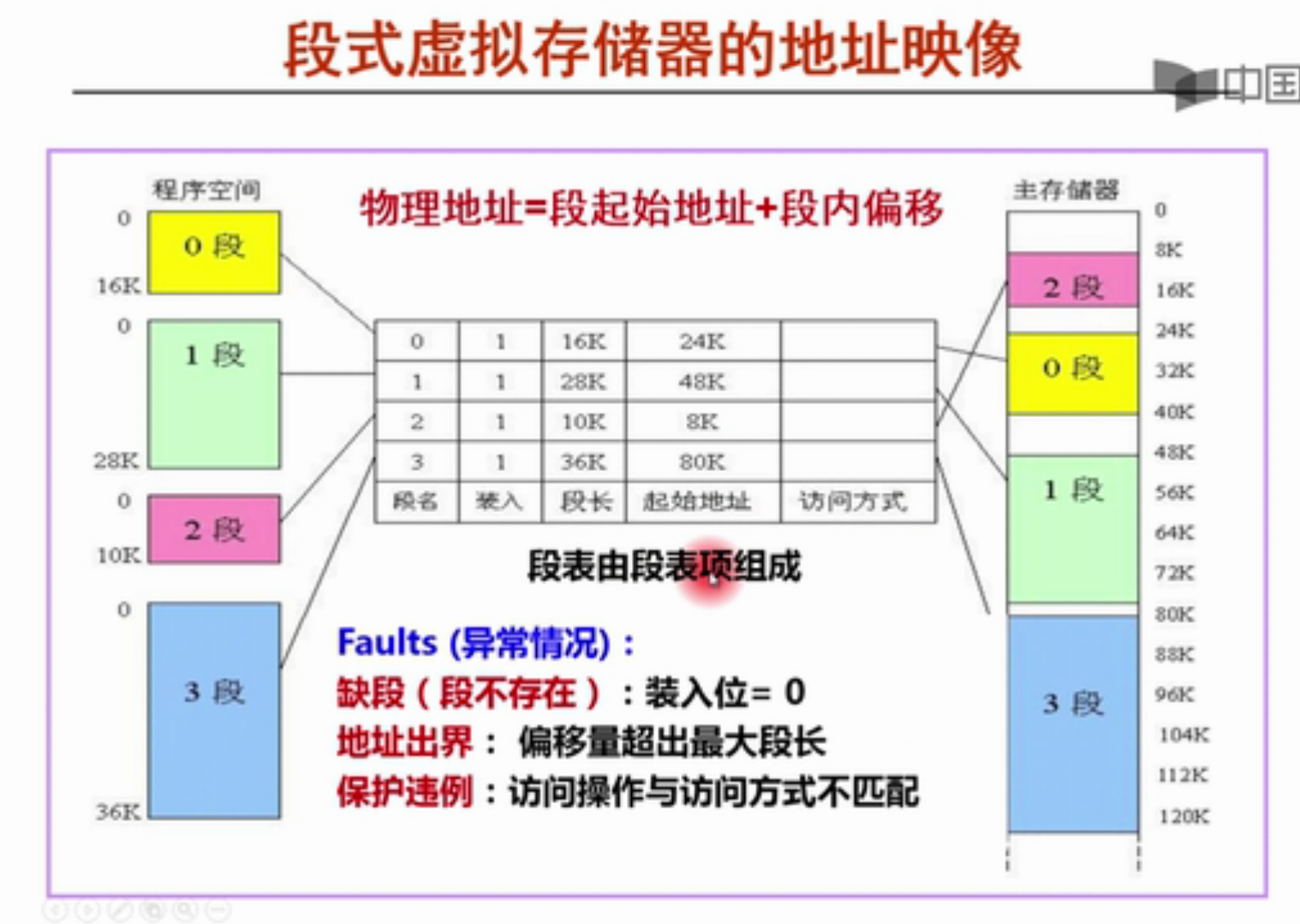
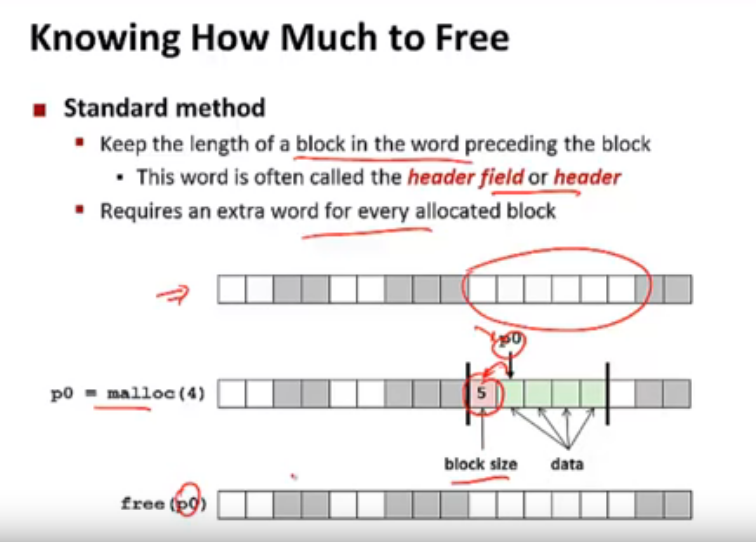
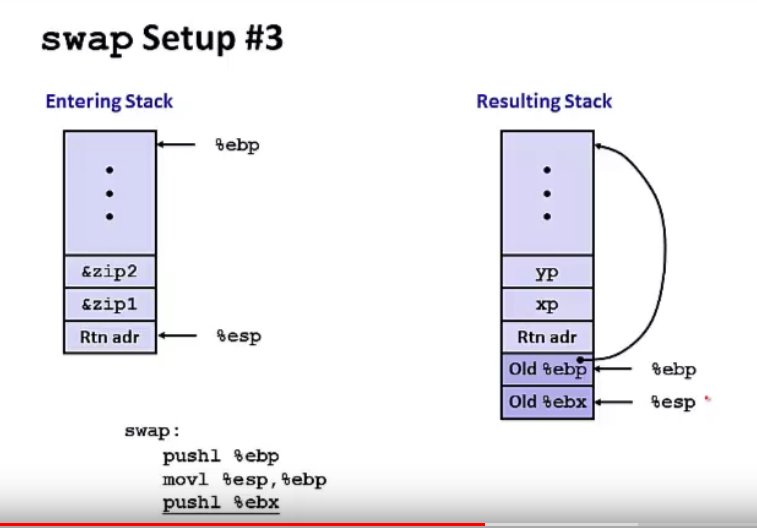
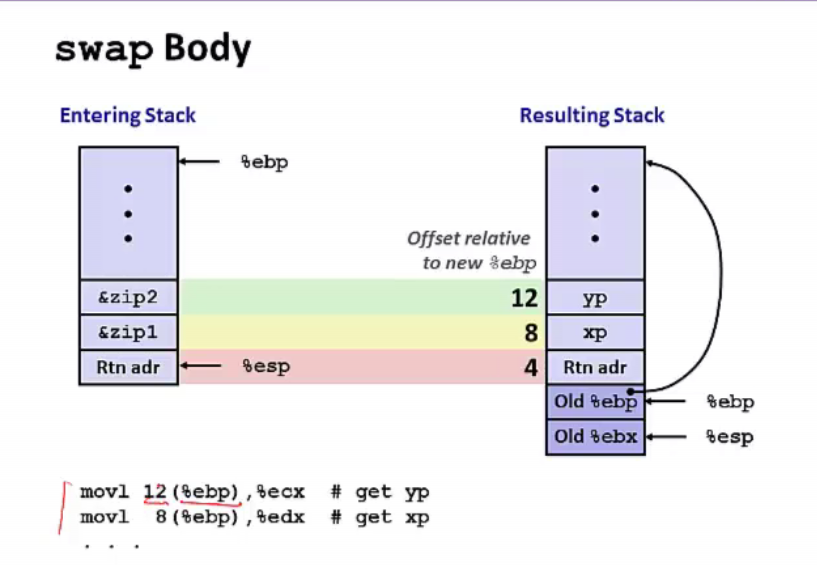
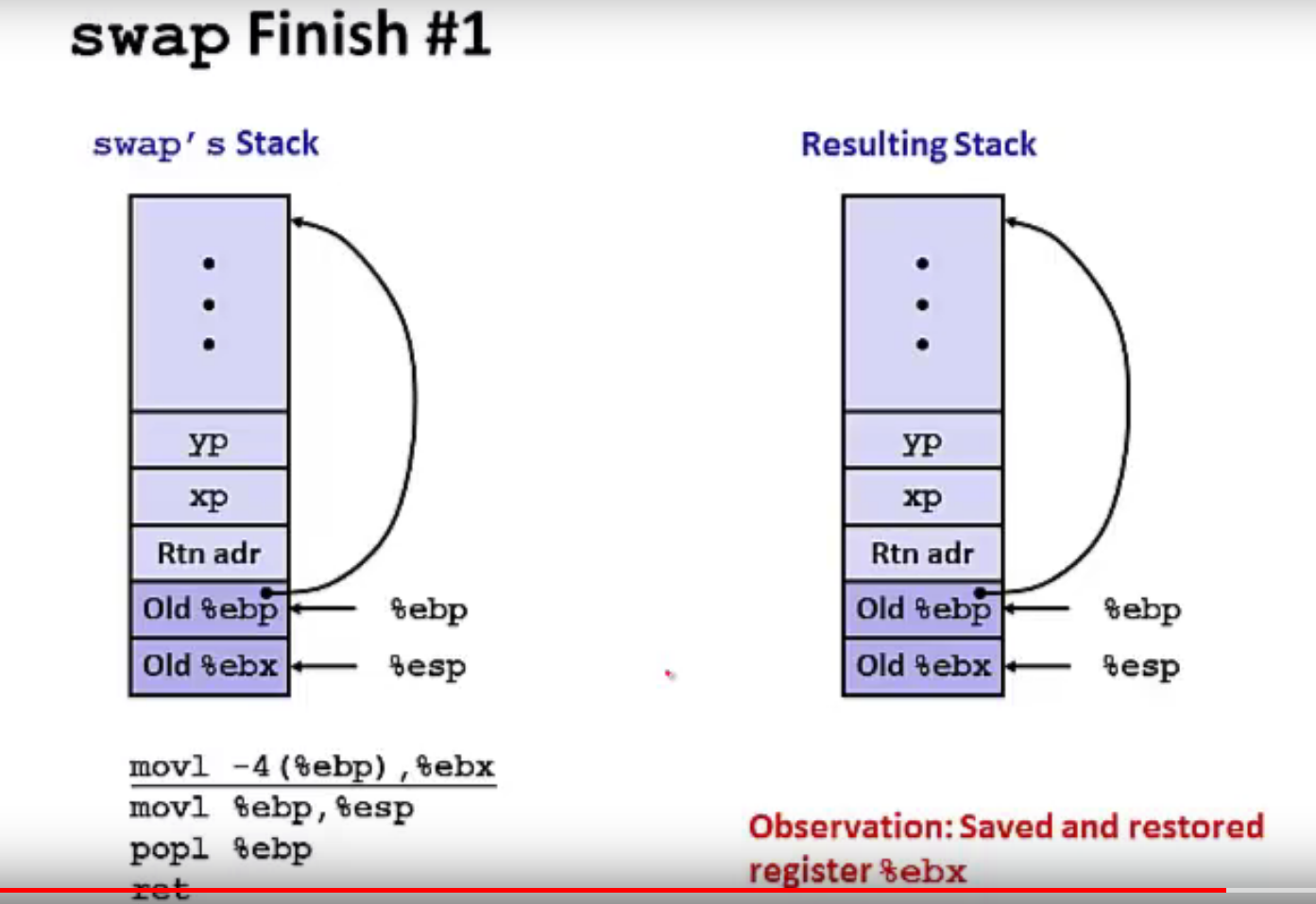
堆的结构:
地址从上到下是从低到高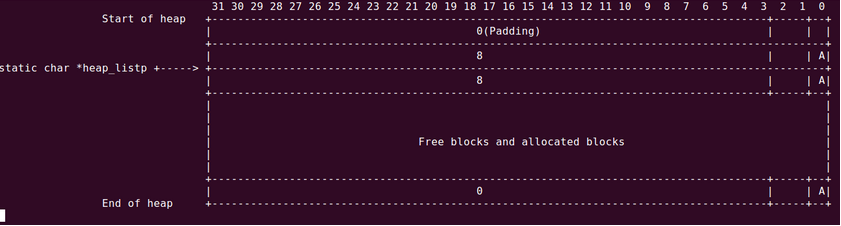
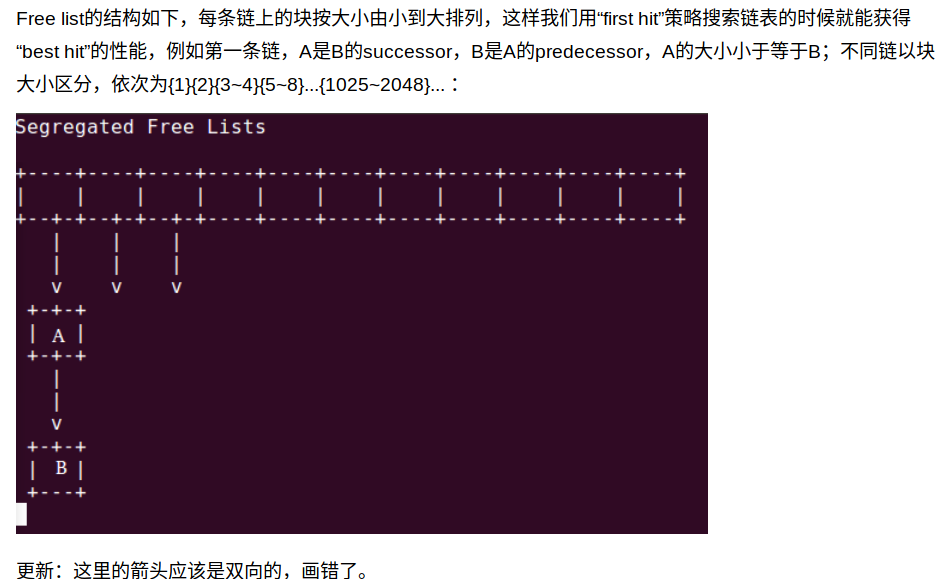
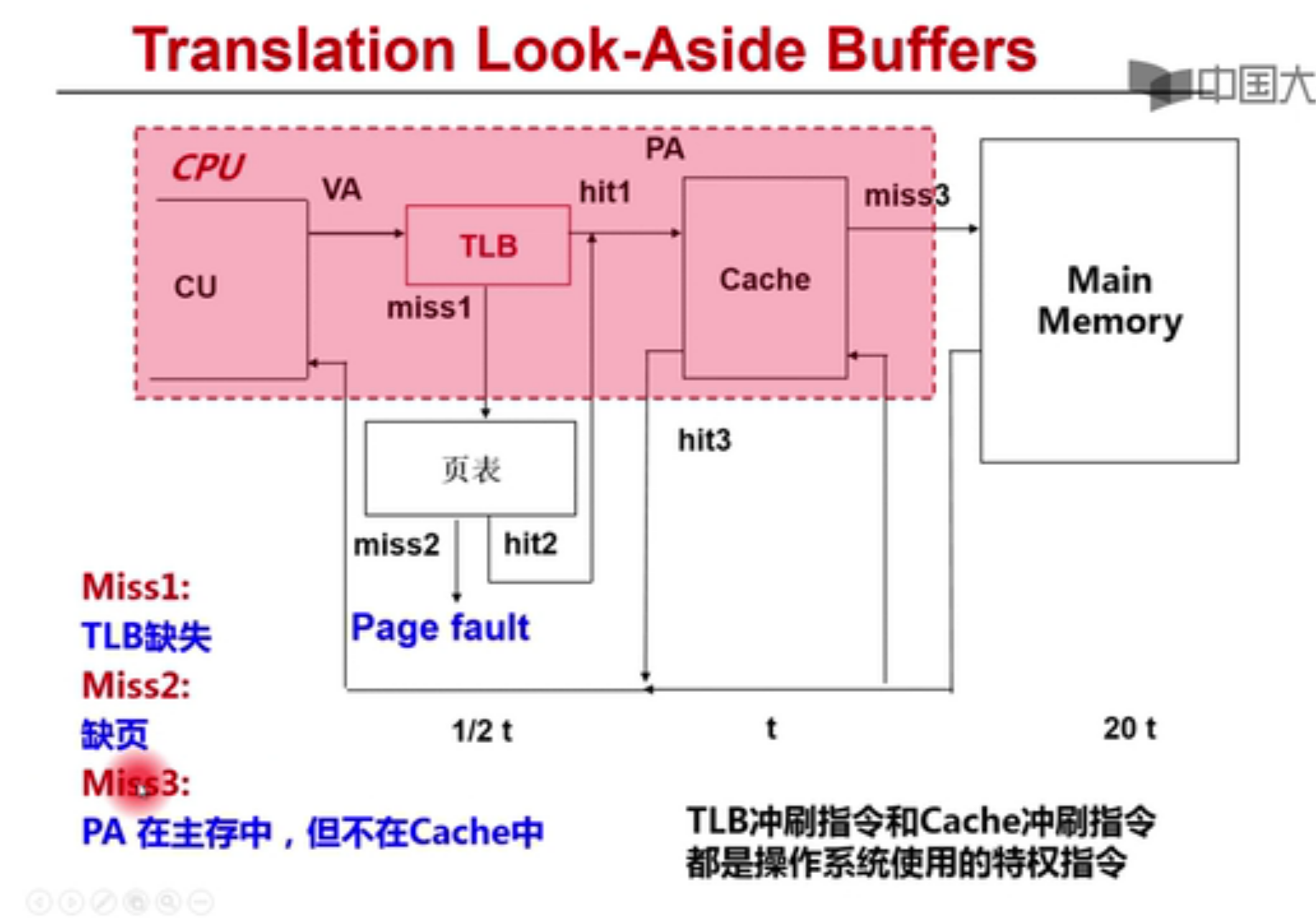
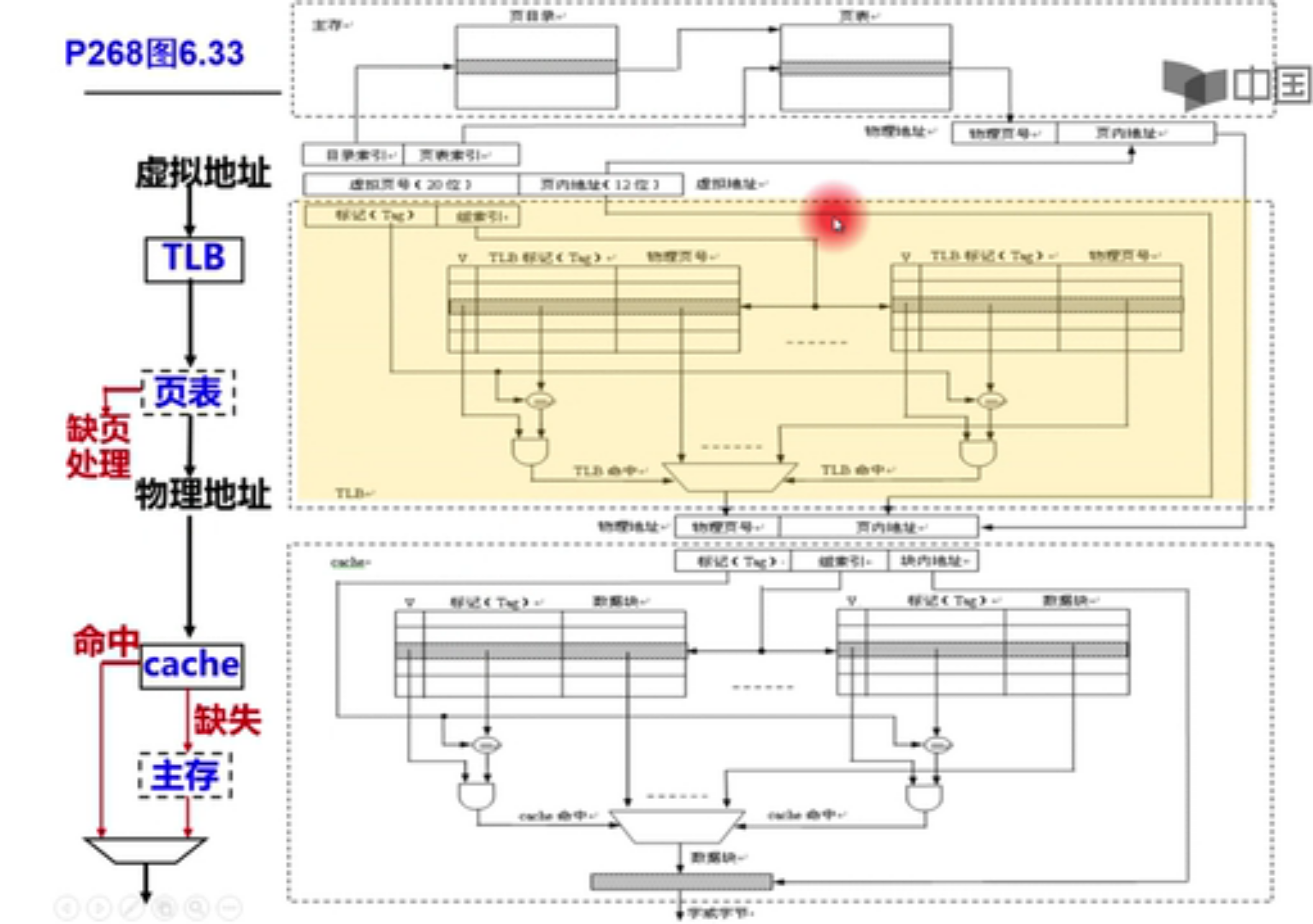
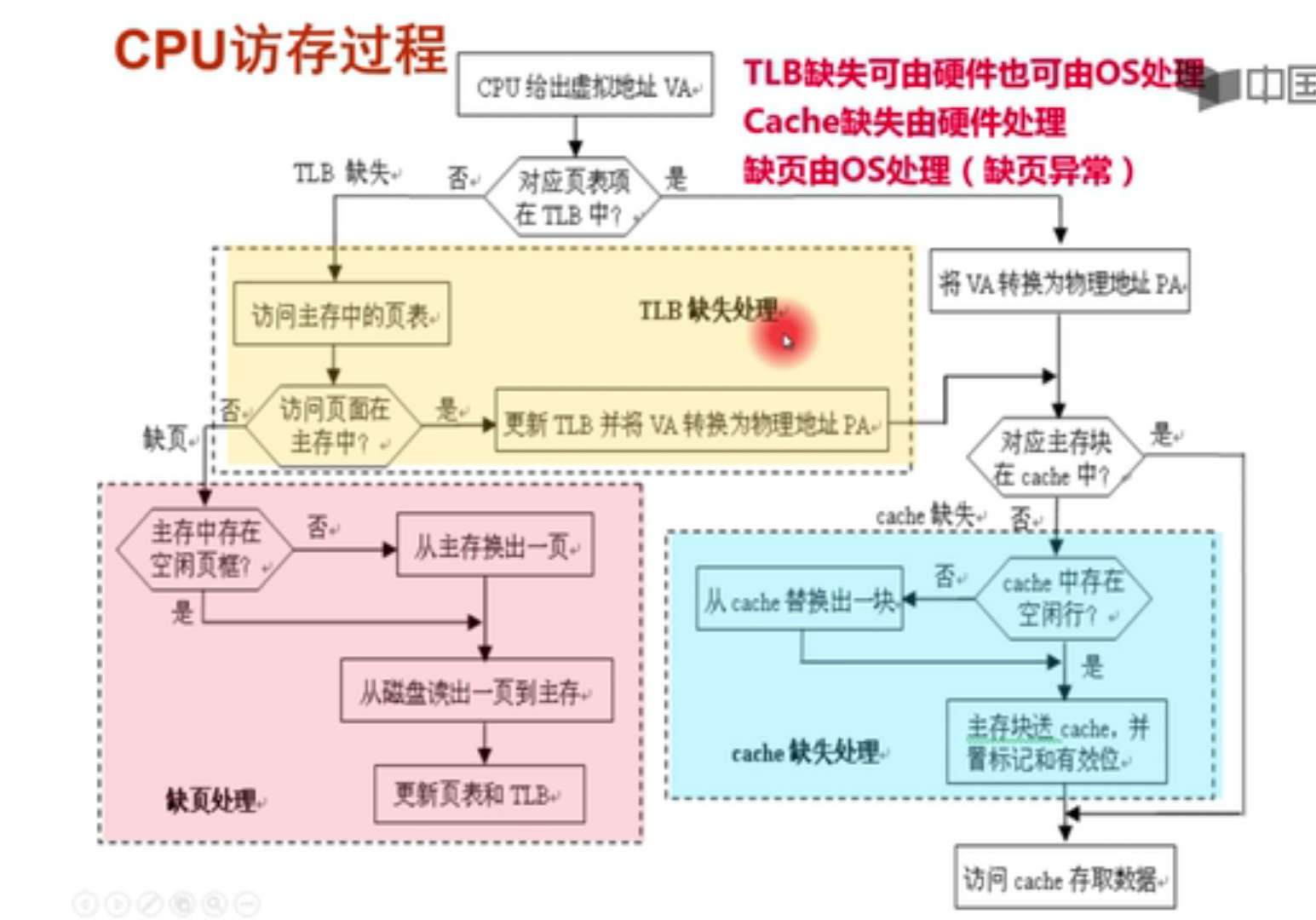
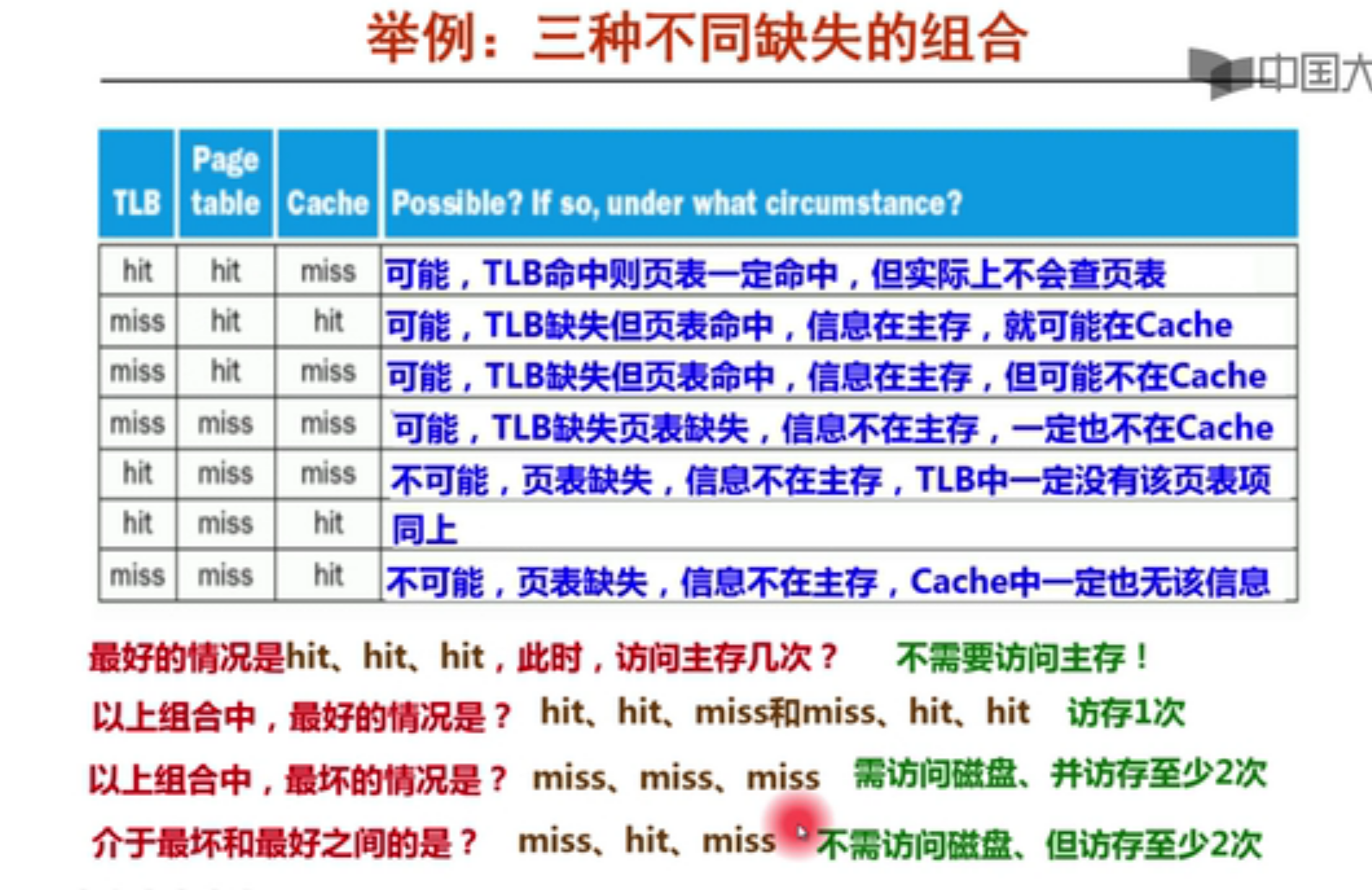
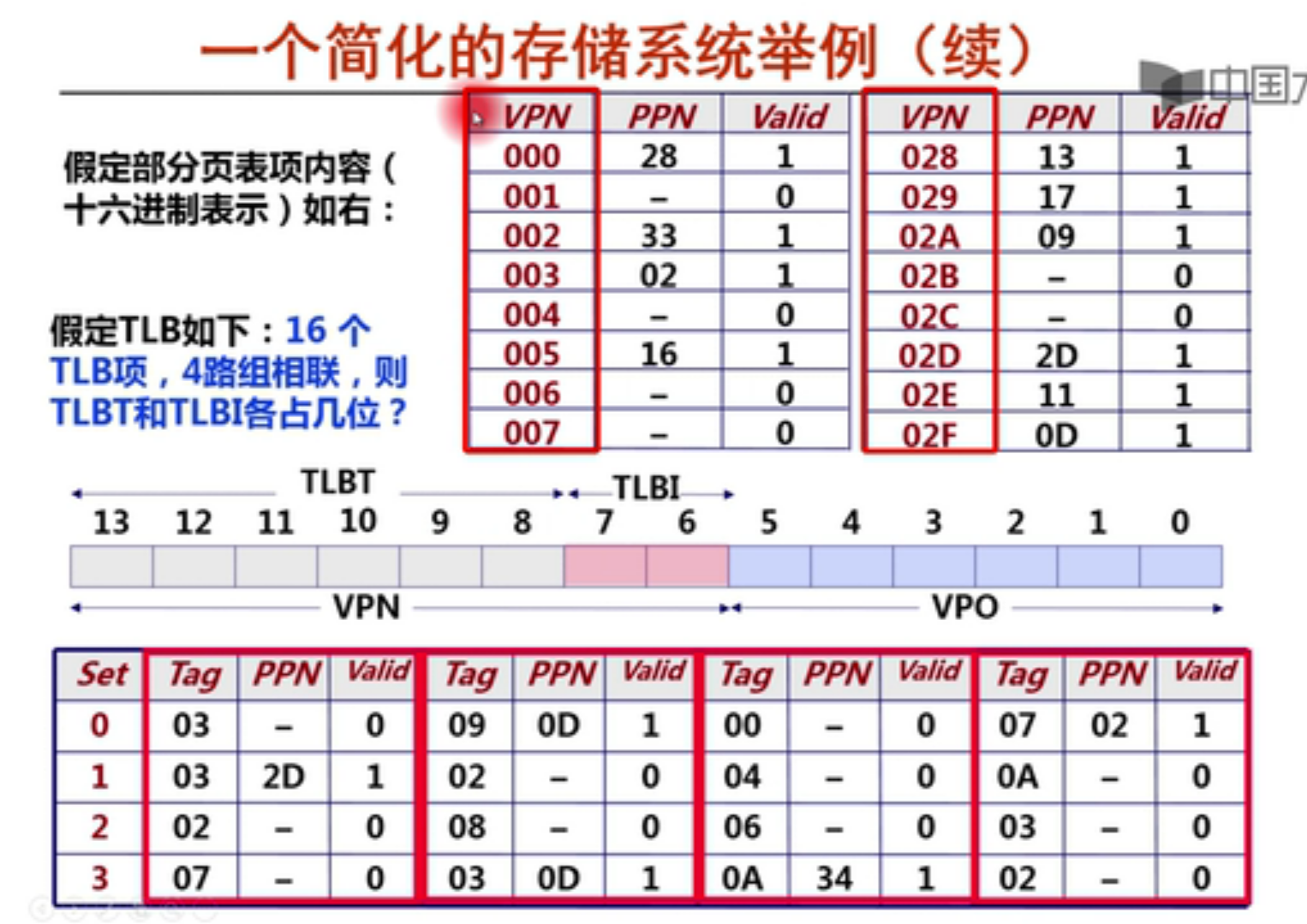
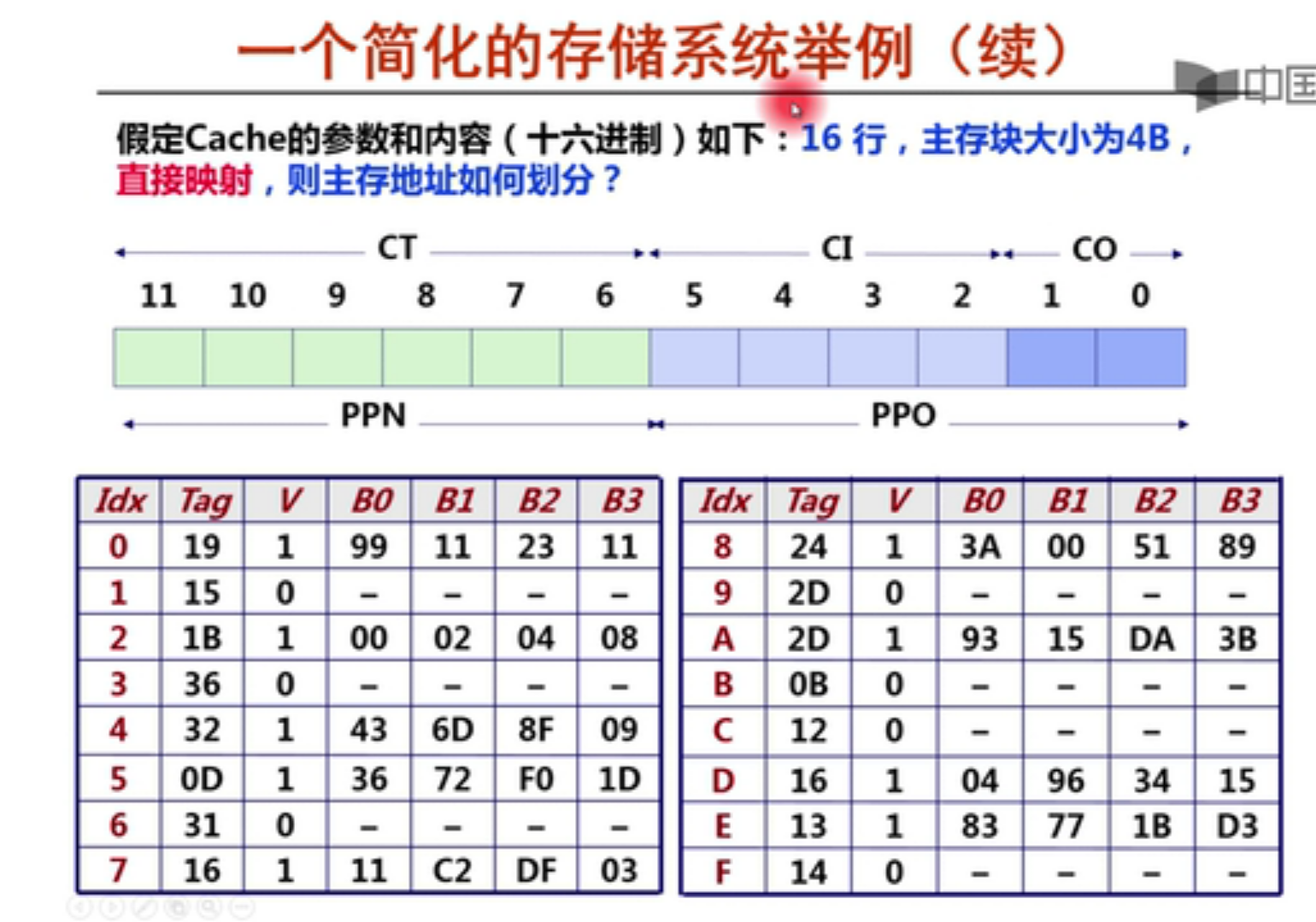
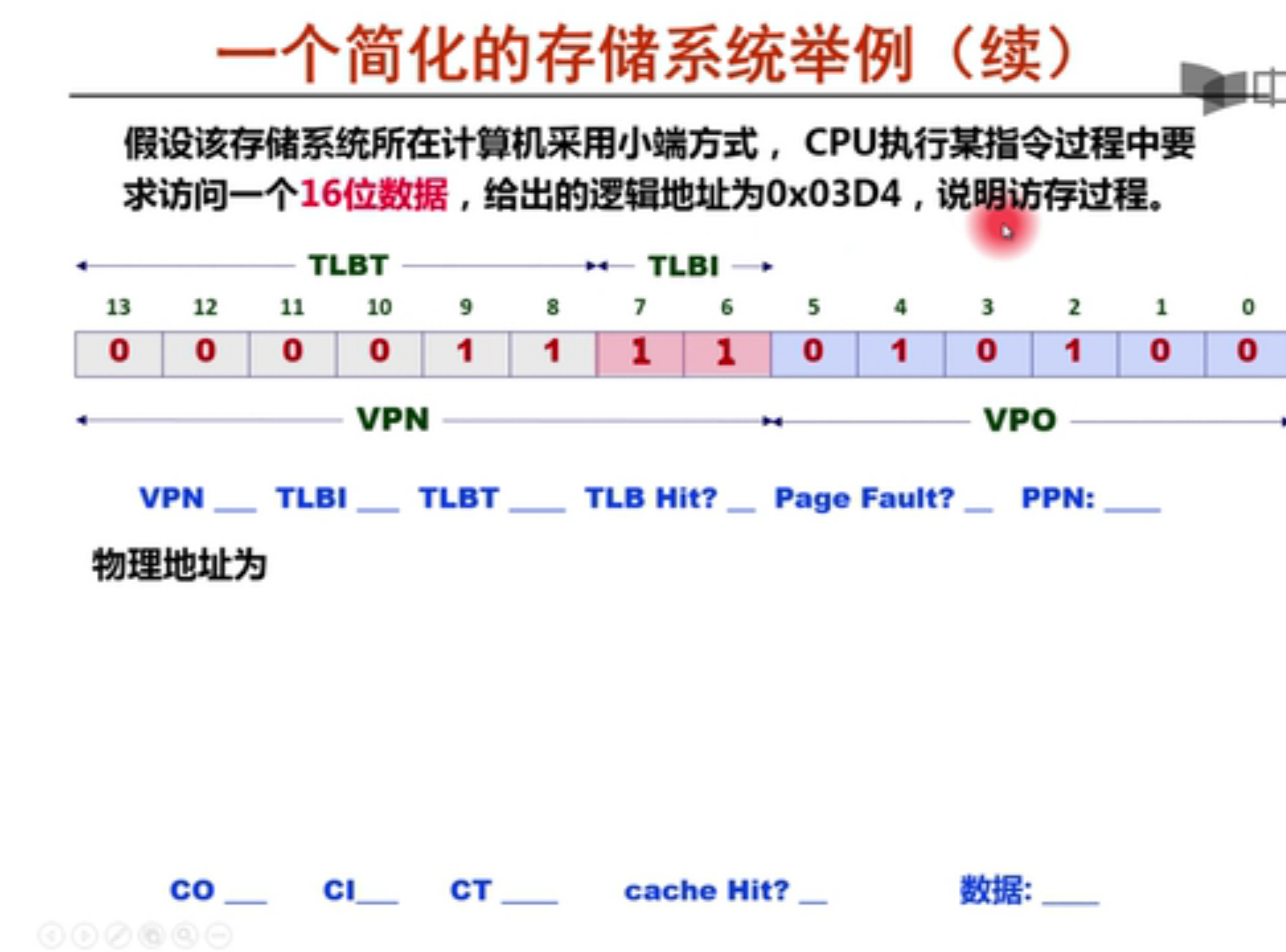
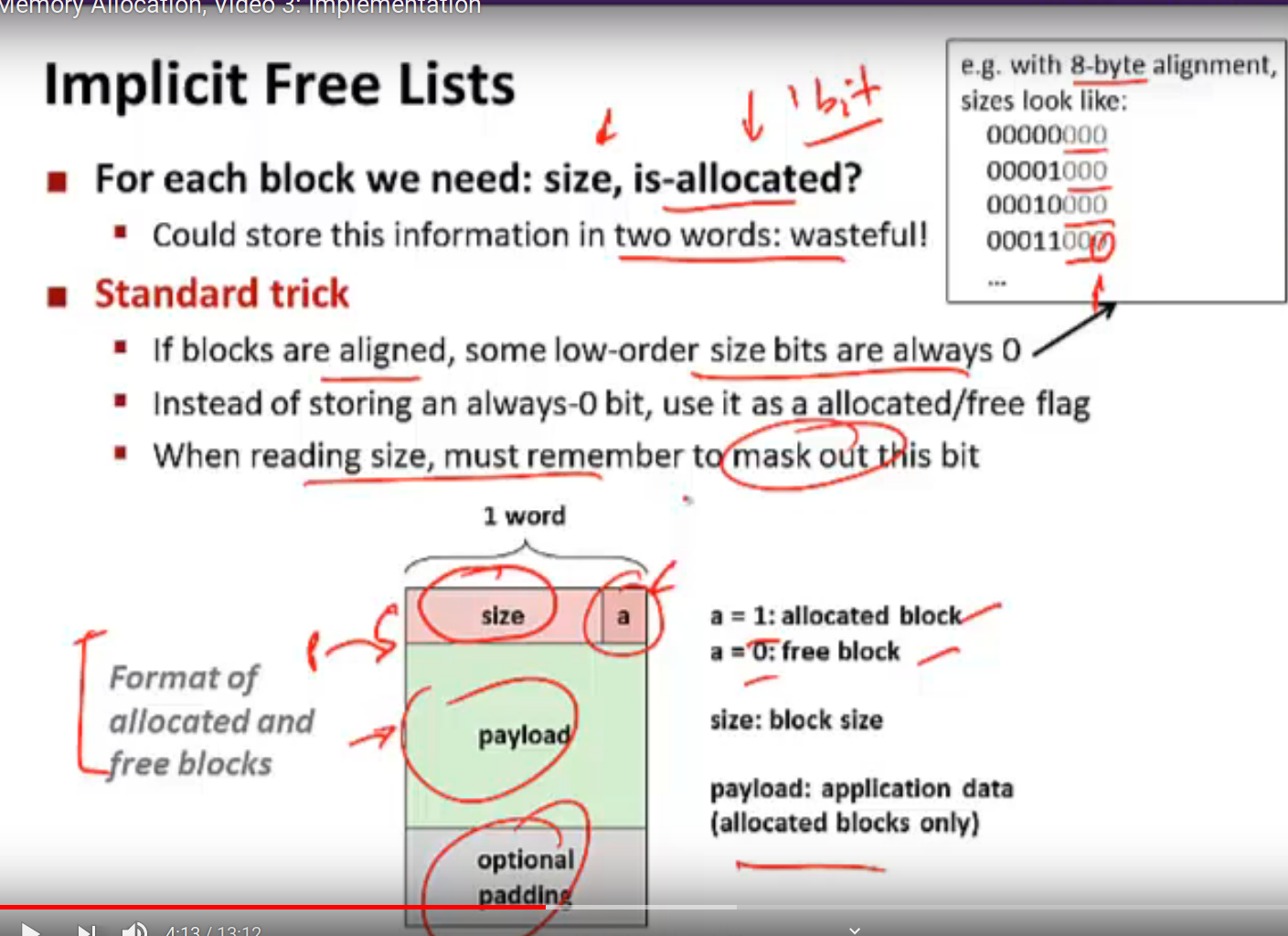
分离适配的原理:
allocator 维护一个空闲链表的数组,每个空闲链表是和一个大小类相关联的,被组织成某种类型的显式或者隐式链表,每个链表包含潜在的大小不同的块。
为了分配,要先确定请求的大小的类,并且对适当的空闲链表做首次适配,如果找到,就分割,并把剩余部分查到空闲链表。如果找不到,就搜索下一个更大的类,如果还是没有,就向操作系统请求额外的堆内存,然后从这个堆内存中分配出一个块,并把剩余部分放在适当的大小类中。
1 | /* single word (4) or double word (8) alignment */ |
全局函数1
2
3
4
5static void *extend_heap(size_t words);
static void *coalesce(void *bp);
static void *place(void *bp,size_t asize);
static void insert(void *bp,size_t size);
static void delete(void *bp);
初始化列表
1 | /* |
1 |
|
1 | void mm_free(void *ptr) |