DL-C5w1HW1

Overview of the model

创建一个基于字符的语言模型

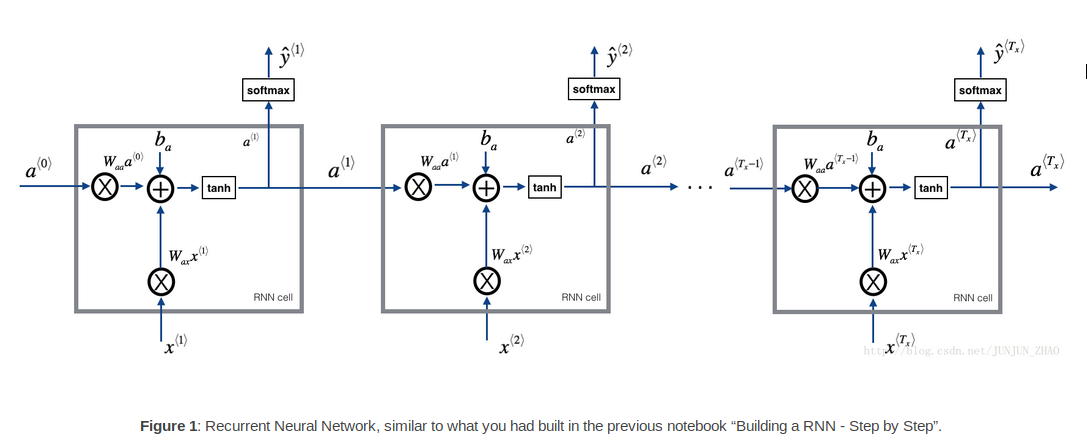
在每一个时间步，RNN基于先前的字符去预测下一个字符是什么，dataset X = {x1,x2,….xT}是输入，而输出Y={y1,y2…yT}使得y^T = x^(T+1)

大概步骤

Initialize parameters
Run the optimization loop
    Forward propagation to compute the loss function
    Backward propagation to compute the gradients with respect to the loss function
    Clip the gradients to avoid exploding gradients
    Using the gradients, update your parameter with the gradient descent update rule.
Return the learned parameters

clip

防止梯度爆炸或者弥散，让所有参数的梯度都限定在一个范围内，如某一个值如果大于maxValue，则这个值设置为maxValue

def clip(gradients, maxValue):
    '''
    Clips the gradients' values between minimum and maximum.
    
    Arguments:
    gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
    maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
    
    Returns: 
    gradients -- a dictionary with the clipped gradients.
    '''
    
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']
   
    for gradient in [dWax, dWaa, dWya, db, dby]:
        np.clip(gradient,-maxValue,maxValue,out=gradient)
    
    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
    
    return gradients

sample

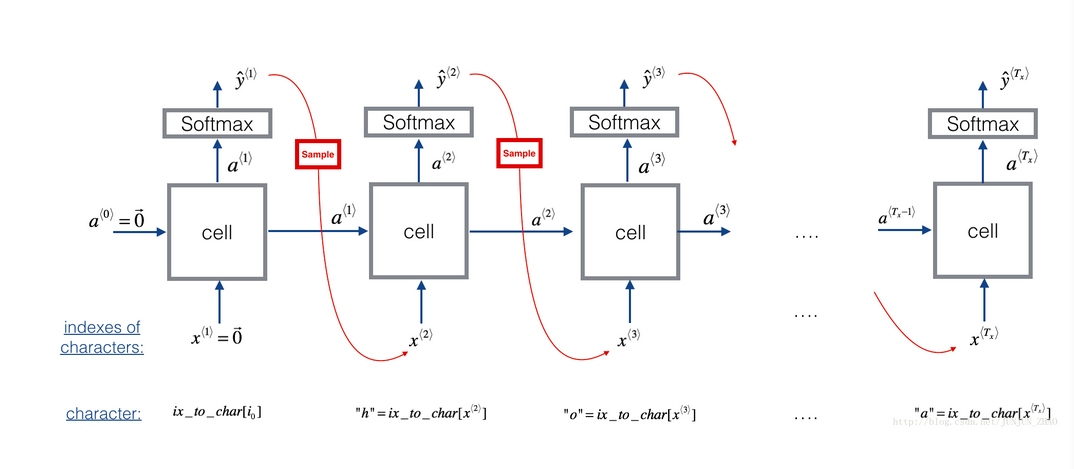
• step1 设置好第0层激活层和第一个输入字符为0向量

• forward propagate

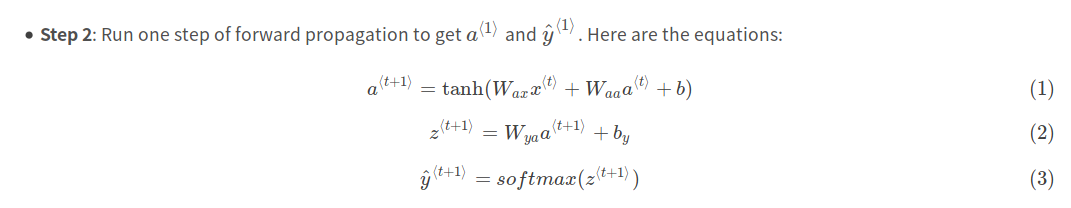
生成一个概率向量，就是这个向量所有数加起来是1，每个数代表着某个字符出现的概率。

• 采样，根据生成的概率向量，选择下一个生成的字符

• 替换x^t的值为x^(t+1)，然后在forward propagate中继续重复这个过程，直到遇到”\n”字符。

def sample(parameters, char_to_ix, seed):
    """
    Sample a sequence of characters according to a sequence of probability distributions output of the RNN

    Arguments:
    parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b. 
    char_to_ix -- python dictionary mapping each character to an index.
    seed -- used for grading purposes. Do not worry about it.

    Returns:
    indices -- a list of length n containing the indices of the sampled characters.
    """
    
    # Retrieve parameters and relevant shapes from "parameters" dictionary
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]
    
    ### START CODE HERE ###
    # Step 1: Create the one-hot vector x for the first character (initializing the sequence generation). (≈1 line)
    x = np.zeros((vocab_size, 1))
    # Step 1': Initialize a_prev as zeros (≈1 line)
    a_prev = np.zeros((n_a, 1))
    
    # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
    indices = []
    
    # Idx is a flag to detect a newline character, we initialize it to -1
    idx = -1 
    
    # Loop over time-steps t. At each time-step, sample a character from a probability distribution and append 
    # its index to "indices". We'll stop if we reach 50 characters (which should be very unlikely with a well 
    # trained model), which helps debugging and prevents entering an infinite loop. 
    counter = 0
    newline_character = char_to_ix['\n']
    
    while (idx != newline_character and counter != 50):
        
        # Step 2: Forward propagate x using the equations (1), (2) and (3)
        a = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
        z = np.dot(Wya, a) + by
        y = softmax(z)
        
        # for grading purposes
        np.random.seed(counter+seed) 
        
        # Step 3: Sample the index of a character within the vocabulary from the probability distribution y
        idx = np.random.choice(list(range(vocab_size)), p = y.ravel())

        # Append the index to "indices"
        indices.append(idx)
        
        # Step 4: Overwrite the input character as the one corresponding to the sampled index.
        x = np.zeros((vocab_size, 1))
        x[idx] = 1
        
        # Update "a_prev" to be "a"
        a_prev = a
        
        # for grading purposes
        seed += 1
        counter +=1
        
    ### END CODE HERE ###

    if (counter == 50):
        indices.append(char_to_ix['\n'])
    
    return indices

Gradient descent

def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
    """
    Execute one step of the optimization to train the model.
    
    Arguments:
    X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
    Y -- list of integers, exactly the same as X but shifted one index to the left.
    a_prev -- previous hidden state.
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        b --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    learning_rate -- learning rate for the model.
    
    Returns:
    loss -- value of the loss function (cross-entropy)
    gradients -- python dictionary containing:
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
                        db -- Gradients of bias vector, of shape (n_a, 1)
                        dby -- Gradients of output bias vector, of shape (n_y, 1)
    a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
    """
    
    ### START CODE HERE ###
    
    # Forward propagate through time (≈1 line)
    loss, cache = rnn_forward(X, Y, a_prev, parameters)
    
    # Backpropagate through time (≈1 line)
    gradients, a = rnn_backward(X, Y, parameters, cache)
    
    # Clip your gradients between -5 (min) and 5 (max) (≈1 line)
    gradients = clip(gradients, maxValue=5)
    
    # Update parameters (≈1 line)
    parameters = update_parameters(parameters, gradients, learning_rate)
    
    ### END CODE HERE ###
    
    return loss, gradients, a[len(X)-1]

model

# GRADED FUNCTION: model

import matplotlib.pyplot as plt
%matplotlib inline


def model(data, ix_to_char, char_to_ix, num_iterations = 50000, n_a = 50, dino_names = 7, vocab_size = 27):
    """
    Trains the model and generates dinosaur names. 
    
    Arguments:
    data -- text corpus
    ix_to_char -- dictionary that maps the index to a character
    char_to_ix -- dictionary that maps a character to an index
    num_iterations -- number of iterations to train the model for
    n_a -- number of units of the RNN cell
    dino_names -- number of dinosaur names you want to sample at each iteration. 
    vocab_size -- number of unique characters found in the text, size of the vocabulary
    
    Returns:
    parameters -- learned parameters
    """
    
    # Retrieve n_x and n_y from vocab_size
    n_x, n_y = vocab_size, vocab_size
    
    # Initialize parameters
    parameters = initialize_parameters(n_a, n_x, n_y)
    
    # Initialize loss (this is required because we want to smooth our loss, don't worry about it)
    loss = get_initial_loss(vocab_size, dino_names)
    
    # Build list of all dinosaur names (training examples).
    with open("names.txt") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]
    
    # Shuffle list of all dinosaur names
    np.random.seed(0)
    np.random.shuffle(examples)
    
    # Initialize the hidden state of your LSTM
    a_prev = np.zeros((n_a, 1))
    
    
    lossList = []
    # Optimization loop
    for j in range(num_iterations):
        
        ### START CODE HERE ###
        
        # Use the hint above to define one training example (X,Y) (≈ 2 lines)
        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]] 
        Y = X[1:] + [char_to_ix["\n"]]
        
        # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
        # Choose a learning rate of 0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
        
        ### END CODE HERE ###
        
        # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
        loss = smooth(loss, curr_loss)
        lossList.append(loss)
        # Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
        if j % 2000 == 0:
            
            print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
            
            # The number of dinosaur names to print
            seed = 0
            for name in range(dino_names):
                
                # Sample indices and print them
                sampled_indices = sample(parameters, char_to_ix, seed)
                print_sample(sampled_indices, ix_to_char)
                
                seed += 1  # To get the same result for grading purposed, increment the seed by one. 
      
            print('\n')
                
    plt.plot(range(num_iterations),lossList)
        
    return parameters

训练数据是88000个英文last name

---

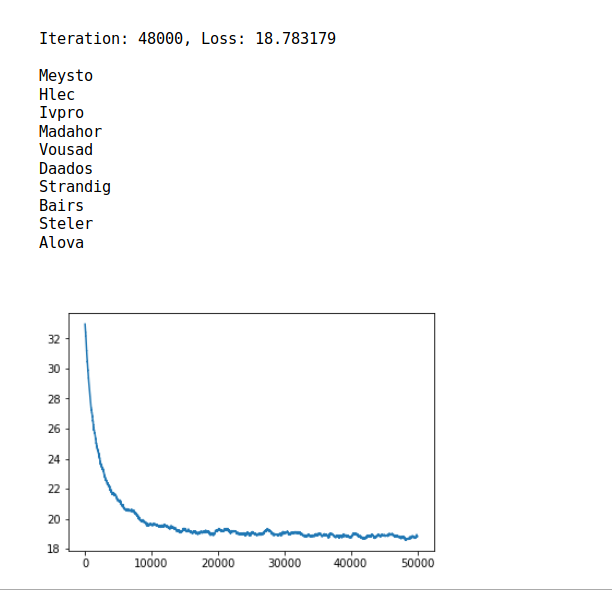
手把手搭建RNN

RNN cell

一个RNN可以看做是一个cell的重复

1.Compute the hidden state with tanh activation: a⟨t⟩=tanh(Waaa⟨t−1⟩+Waxx⟨t⟩+ba).
2.Using your new hidden state a⟨t⟩, compute the prediction ŷ ⟨t⟩=softmax(Wyaa⟨t⟩+by). We provided you a function: softmax.
3.Store (a⟨t⟩,a⟨t−1⟩,x⟨t⟩,parameters) in cache
4.Return a⟨t⟩ , y⟨t⟩  and cache

    
def rnn_cell_forward(xt, a_prev, parameters):
    """
    Implements a single forward step of the RNN-cell as described in Figure (2)

    Arguments:
    xt -- your input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
    """
    
    # Retrieve parameters from "parameters"
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    ### START CODE HERE ### (≈2 lines)
    # compute next activation state using the formula given above
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    # compute output of the current cell using the formula given above
    yt_pred = softmax(np.dot(Wya, a_next) + by)
    ### END CODE HERE ###
    
    # store values you need for backward propagation in cache
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache

RNN forward

def rnn_forward(x, a0, parameters):
    """
    Implement the forward propagation of the recurrent neural network described in Figure (3).

    Arguments:
    x -- Input data for every time-step, of shape (n_x, m, T_x).
    a0 -- Initial hidden state, of shape (n_a, m)
    parameters -- python dictionary containing:
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        ba --  Bias numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)

    Returns:
    a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
    y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
    caches -- tuple of values needed for the backward pass, contains (list of caches, x)
    """
    
    # Initialize "caches" which will contain the list of all caches
    caches = []
    
    # Retrieve dimensions from shapes of x and Wy
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
    
    ### START CODE HERE ###
    
    # initialize "a" and "y" with zeros (≈2 lines)
    a = np.zeros((n_a,m,T_x))
    y_pred= np.zeros((n_y,m,T_x))
    # Initialize a_next (≈1 line)
    a_next = a0
    
    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, compute the prediction, get the cache (≈1 line)
        a_next,yt_pred,cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
        # Save the value of the new "next" hidden state in a (≈1 line)
        a[:,:,t] = a_next
        # Save the value of the prediction in y (≈1 line)
        y_pred[:,:,t] = yt_pred
        # Append "cache" to "caches" (≈1 line)
        caches.append(cache)
    ### END CODE HERE ###
    
    # store values needed for backward propagation in cache
    caches = (caches, x)
    
    return a, y_pred, caches

LSTM

遗忘门

我们假设我们正在阅读一段文本中的单词, 并希望使用 LSTM 来跟踪语法结构, 例如主语是单数还是复数。如果主语从一个单数词变为复数词, 我们需要找到一种方法来去除以前存储的单数/复数状态的内存值。在 LSTM 中, 遗忘门让我们这样做:

更新门

输出门

# GRADED FUNCTION: lstm_cell_forward

def lstm_cell_forward(xt, a_prev, c_prev, parameters):
    """
    Implement a single forward step of the LSTM-cell as described in Figure (4)

    Arguments:
    xt -- your input data at timestep "t", numpy array of shape (n_x, m).
    a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
    c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
                        Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        bi -- Bias of the update gate, numpy array of shape (n_a, 1)
                        Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
                        bc --  Bias of the first "tanh", numpy array of shape (n_a, 1)
                        Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
                        bo --  Bias of the output gate, numpy array of shape (n_a, 1)
                        Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
                        
    Returns:
    a_next -- next hidden state, of shape (n_a, m)
    c_next -- next memory state, of shape (n_a, m)
    yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
    cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters)
    
    Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde),
          c stands for the memory value
    """

    # Retrieve parameters from "parameters"
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]
    
    # Retrieve dimensions from shapes of xt and Wy
    n_x, m = xt.shape
    n_y, n_a = Wy.shape

    ### START CODE HERE ###
    # Concatenate a_prev and xt (≈3 lines)
    concat = np.zeros((n_a+n_x,m))
    concat[:n_a,:] = a_prev
    concat[n_a:,:] = xt
    # Compute values for ft, it, cct, c_next, ot, a_next using the formulas given figure (4) (≈6 lines)
    ft = sigmoid(np.dot(Wf,concat)+bf)
    it = sigmoid(np.dot(Wi,concat)+bi)
    cct = np.tanh(np.dot(Wc,concat)+bc)
    c_next = ft*c_prev+it*cct
    ot = sigmoid(np.dot(Wo,concat)+bo)
    a_next = ot*np.tanh(c_next)
    # Compute prediction of the LSTM cell (≈1 line)
    yt_pred = softmax(np.dot(Wy,a_next)+by)
    ### END CODE HERE ###

    # store values needed for backward propagation in cache
    cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)

    return a_next, c_next, yt_pred, cache

def lstm_forward(x, a0, parameters):
    """
    Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (3).

    Arguments:
    x -- Input data for every time-step, of shape (n_x, m, T_x).
    a0 -- Initial hidden state, of shape (n_a, m)
    parameters -- python dictionary containing:
                        Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        bf -- Bias of the forget gate, numpy array of shape (n_a, 1)
                        Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x)
                        bi -- Bias of the update gate, numpy array of shape (n_a, 1)
                        Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x)
                        bc -- Bias of the first "tanh", numpy array of shape (n_a, 1)
                        Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x)
                        bo -- Bias of the output gate, numpy array of shape (n_a, 1)
                        Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
                        
    Returns:
    a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
    y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
    caches -- tuple of values needed for the backward pass, contains (list of all the caches, x)
    """

    # Initialize "caches", which will track the list of all the caches
    caches = []
    
    ### START CODE HERE ###
    # Retrieve dimensions from shapes of x and Wy (≈2 lines)
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wy"].shape
    
    # initialize "a", "c" and "y" with zeros (≈3 lines)
    a = np.zeros((n_a, m, T_x))
    c = a
    y = np.zeros((n_y, m, T_x))
    
    # Initialize a_next and c_next (≈2 lines)
    a_next = a0
    c_next = np.zeros(a_next.shape)
    
    # loop over all time-steps
    for t in range(T_x):
        # Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
        a_next, c_next, yt, cache = lstm_cell_forward(x[:,:,t], a_next, c_next, parameters)
        # Save the value of the new "next" hidden state in a (≈1 line)
        a[:,:,t] = a_next
        # Save the value of the prediction in y (≈1 line)
        y[:,:,t] = yt
        # Save the value of the next cell state (≈1 line)
        c[:,:,t]  = c_next
        # Append the cache into caches (≈1 line)
        caches.append(cache)
        
    ### END CODE HERE ###
    
    # store values needed for backward propagation in cache
    caches = (caches, x)

    return a, y, c, caches

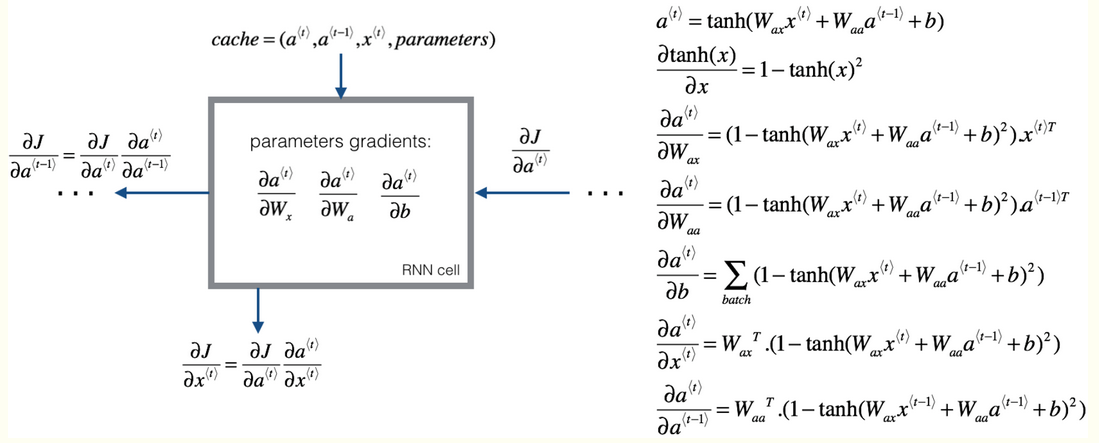
RNN backward pass

LSTM music generation

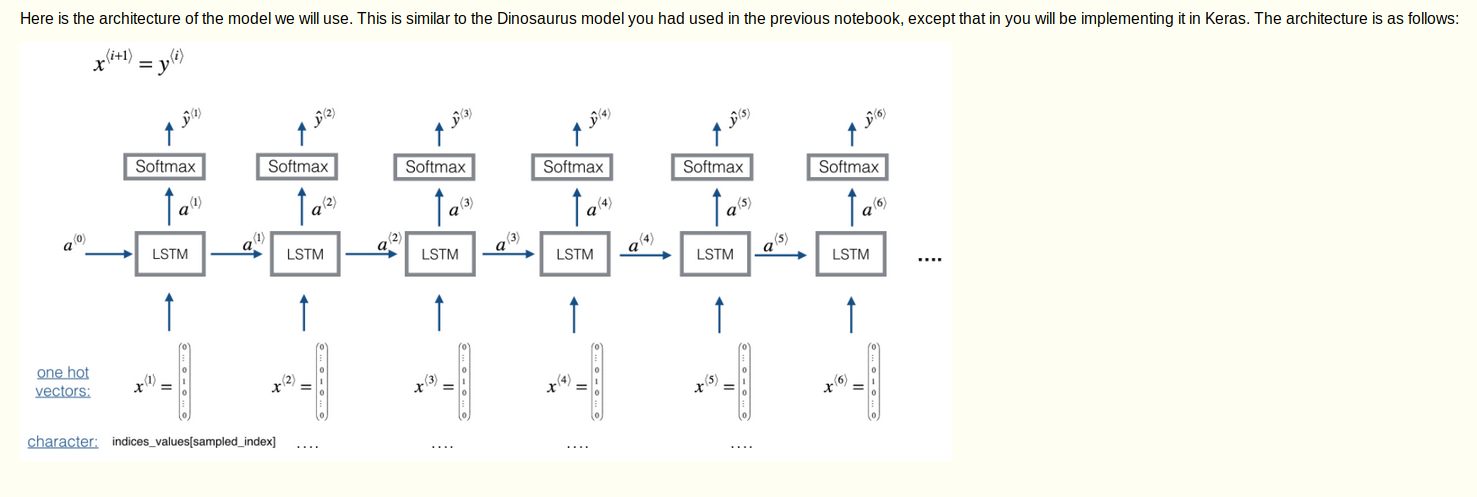
从一个更长的序列中随机选取30个数值片段来训练模型，因此不会设置x(1) 为 零向量。 设置每个片段都有相同长度Tx=30，使得矢量化更容易。

building model

对于序列生成，测试的时候不能提前知道所有的x^t数值，而使用x^t = y^(t-1)一次生成一个，因此要实现for循环来访问不同的时间步，函数djmodel()将使用for循环调用LSTM层TX T次，并且每次第Tx步都应该有共享权重，而不应该重新初始化权重。

在Keras中实现具有共享权重层的关键步骤

1.定义层对象

2.前向传播输入时候调用这些对象

n_a = 64 
reshapor = Reshape((1, n_values))
LSTM_cell = LSTM(n_a, return_state = True)
Densor = Dense(n_values, activation='softmax')

def create_model(Tx, n_a, n_values):
    """
    Implement the model
    
    Arguments:
    Tx -- length of the sequence in a corpus
    n_a -- the number of activations used in our model
    n_values -- number of unique values in the music data 
    
    Returns:
    model -- a keras model with the 
    """
    
    # Define the input of your model with a shape 
    X = Input(shape=(Tx, n_values))
    
    # Define s0, initial hidden state for the decoder LSTM
    a0 = Input(shape=(n_a,), name='a0')
    c0 = Input(shape=(n_a,), name='c0')
    a = a0
    c = c0
    
    # Step 1: Create empty list to append the outputs while you iterate (≈1 line)
    output = []
    
    # Step 2: Loop
    for t in range(Tx):
        
        # Step 2.A: select the "t"th time step vector from X. 
        x = Lambda(lambda x:X[:,t,:])(X)
        # Step 2.B: Use reshapor to reshape x to be (1, n_values) (≈1 line)
        x = reshapor(x)
        # Step 2.C: Perform one step of the LSTM_cell
        a,_,c = LSTM_cell(x,initial_state = [a,c])
        # Step 2.D: Apply densor to the hidden state output of LSTM_Cell
        out = Densor(a)
        # Step 2.E: add the output to "outputs"
        output.append(out)
    # Step 3: Create model instance
    model = Model([X,a0,c0],output)
    
    return model

model = create_model(Tx = 30 , n_a = n_a, n_values = n_values)

opt = Adam(lr=0.1, beta_1=0.9, beta_2=0.999, decay=0.003)

model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])

m = 60
a0 = np.zeros((m,n_a))
c0 = np.zeros((m,n_a))
model.fit([X, a0, c0], list(Y), epochs=500)

LSTM

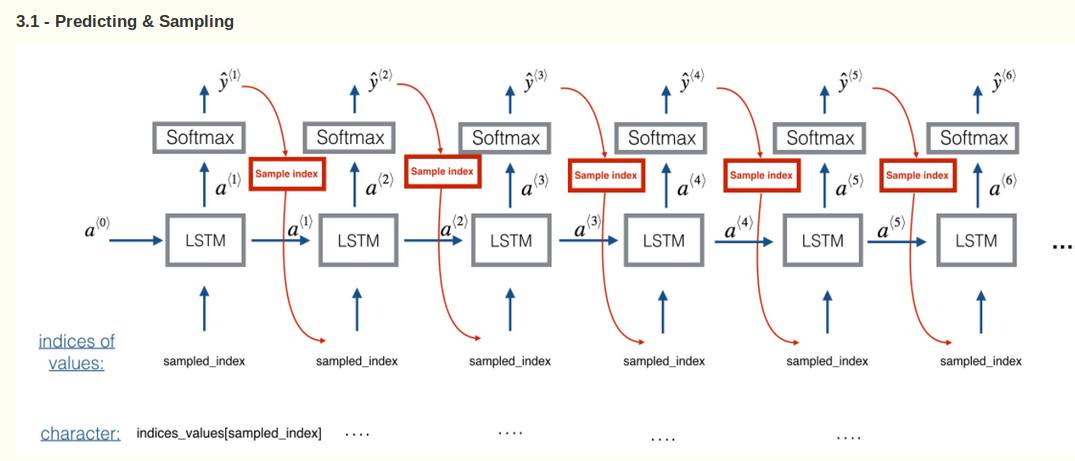
用上个cell预测的值来作为下个cell的输入值

def music_inference_model(LSTM_cell, densor, n_values = n_values, n_a = 64, Ty = 100):
    """
    Uses the trained "LSTM_cell" and "densor" from model() to generate a sequence of values.
    
    Arguments:
    LSTM_cell -- the trained "LSTM_cell" from model(), Keras layer object
    densor -- the trained "densor" from model(), Keras layer object
    n_values -- integer, umber of unique values
    n_a -- number of units in the LSTM_cell
    Ty -- integer, number of time steps to generate
    
    Returns:
    inference_model -- Keras model instance
    """
    
    # Define the input of your model with a shape 
    x0 = Input(shape=(1, n_values))
    
    # Define s0, initial hidden state for the decoder LSTM
    a0 = Input(shape=(n_a,), name='a0')
    c0 = Input(shape=(n_a,), name='c0')
    a = a0
    c = c0
    x = x0

    # Step 1: Create an empty list of "outputs" to later store your predicted values (≈1 line)
    outputs = []
    
    # Step 2: Loop over Ty and generate a value at every time step
    for t in range(Ty):
        
        # Step 2.A: Perform one step of LSTM_cell (≈1 line)
        a, _, c = LSTM_cell(x, initial_state=[a, c])
        
        # Step 2.B: Apply Dense layer to the hidden state output of the LSTM_cell (≈1 line)
        out = densor(a)

        # Step 2.C: Append the prediction "out" to "outputs". out.shape = (None, 78) (≈1 line)
        outputs.append(out)
        
        # Step 2.D: Select the next value according to "out", and set "x" to be the one-hot representation of the
        #           selected value, which will be passed as the input to LSTM_cell on the next step. We have provided 
        #           the line of code you need to do this. 
        x = Lambda(one_hot)(out)
        
    # Step 3: Create model instance with the correct "inputs" and "outputs" (≈1 line)
    inference_model = Model(inputs = [x0, a0, c0], outputs = outputs)
    
    return inference_model