DL-C4W1

为什么要卷积？

for big size picture, the input scale would be very large. eg. an 10001000 size picture,
after flattening its features , you can get a vector as (31000*1000,1) = (3million ,1)

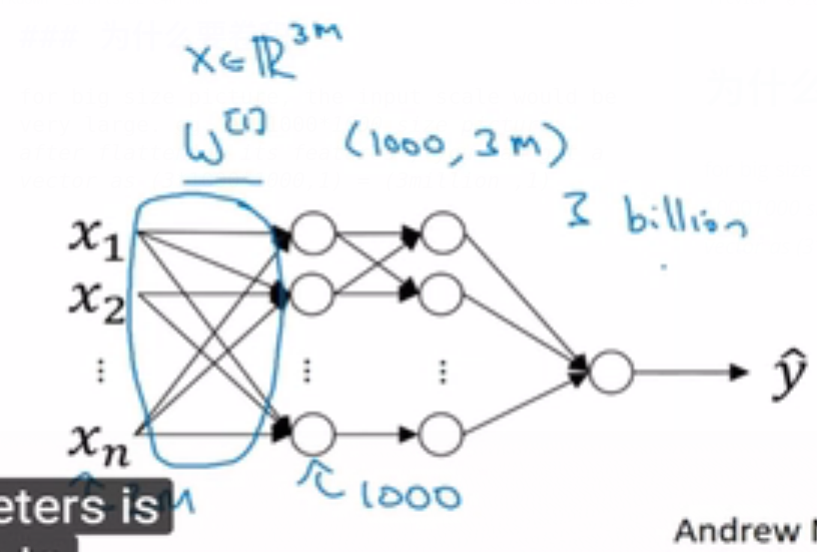
如果hidden　layer只有1000层，那么W1 的输入大小是(1000,3m)

因为z(1000,1) = W1(1000,3M)*X(3M,1)+b

边缘检测

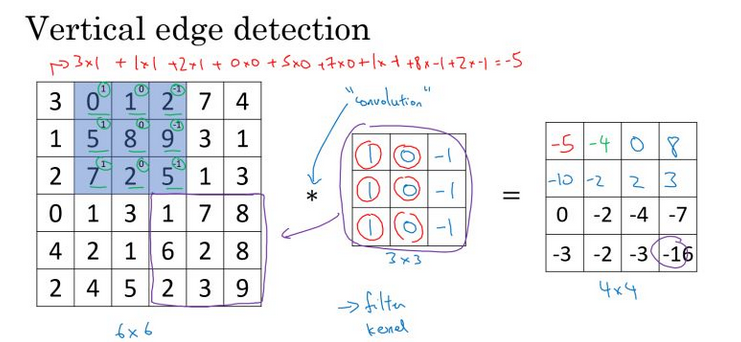
用一个33大小的卷积核对一张66大小的图片进行卷积运算，最终得到一个4x4的图片

python:conv_forward

tf.nn.conv2d

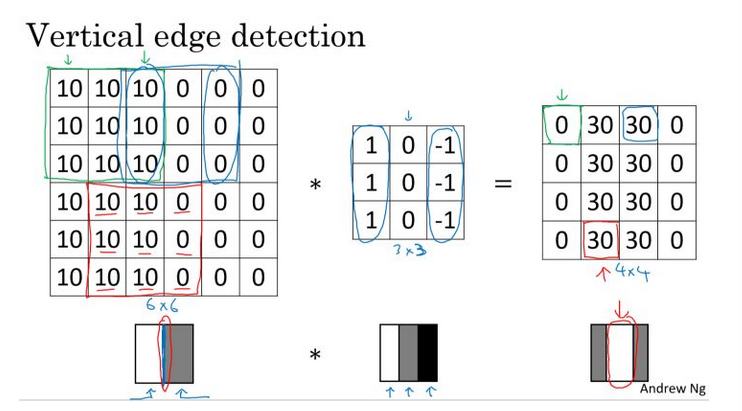
边缘检测原理

用垂直边缘filter，可以明显吧边缘和非边缘区区分出来。

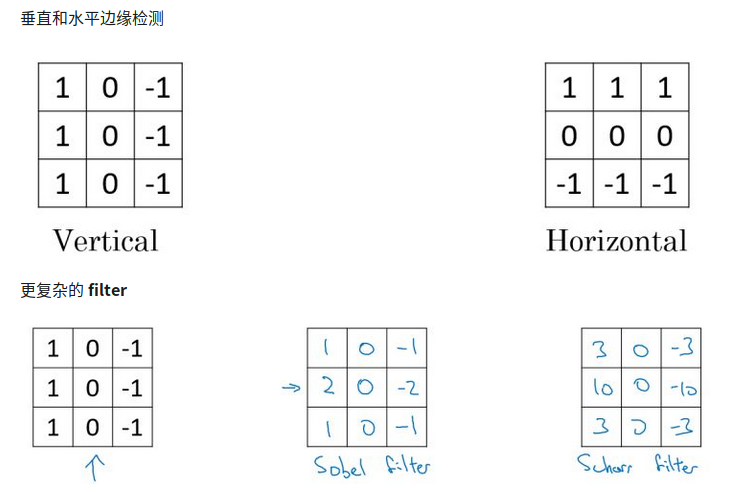
多种边缘检测

我们可以直接把filter中的数字直接看作是需要学习的参数

在nn中通过反向传播算法，学习到相应于目标结果的filter，然后把其应用在整个图片上，输出其提取到的所有有用的特征。

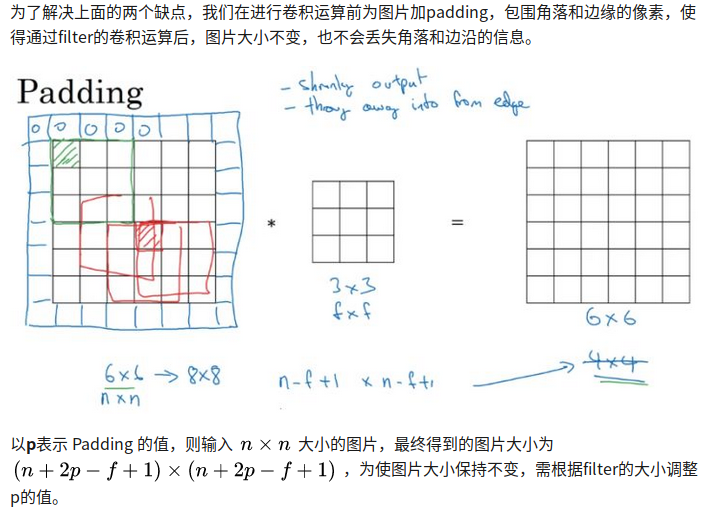
padding

从上面注意到每次卷积操作，图片会缩小。

所以我们要在卷积之前，为图片加padding，包围角落和边缘的像素，使得通过filter的卷积运算后，图片大小不变，也不会丢失角落。

valid/Some 卷积

Valid: no padding

nxn –>(n-f+1)x(n-f+1)

Same: padding

输出和输入图片的大小相同

p = (f-1)/2，在CV中，一般来说padding的值位奇数

N+2P-F+1 = N ,SO p = (F-1)/2

卷积步长（stride）

stride=1,表示每次卷积运算以一个步长进行移动。

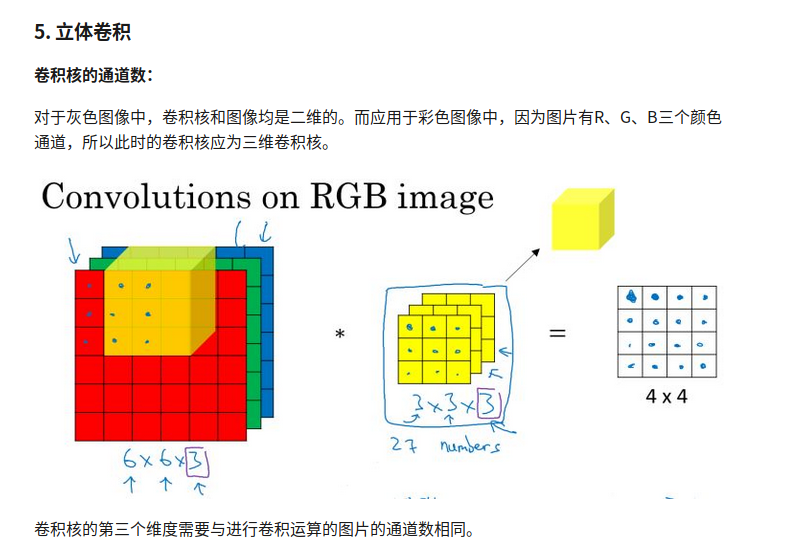
立体卷积

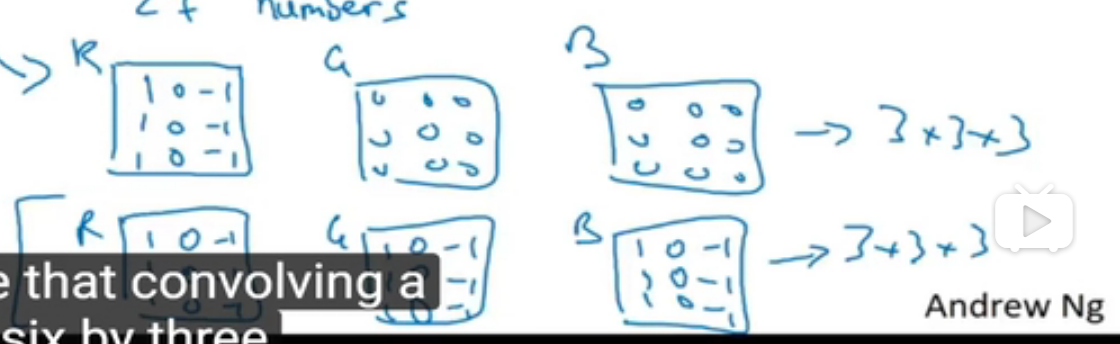
第一行表示只检测红色通道的垂直边缘

第二行表示检测所有通道垂直边缘

卷积核第三个维度大小等于图片通道大小

多卷积

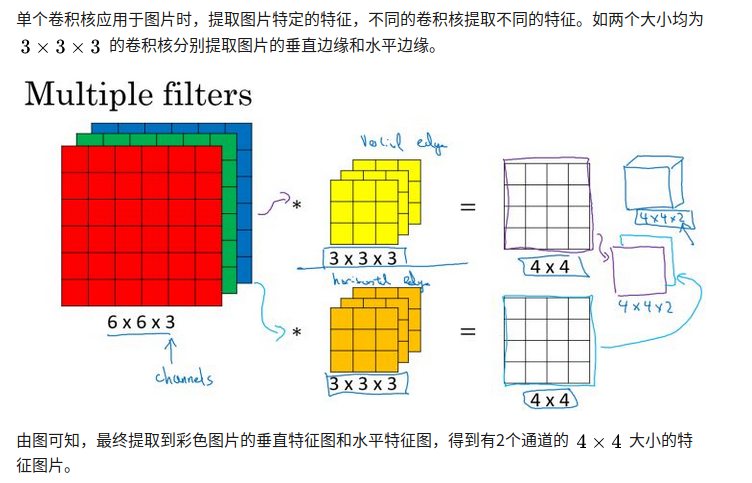
上图意思是把检测垂直和水平边缘的两个图片叠成两层。

单层卷积网络

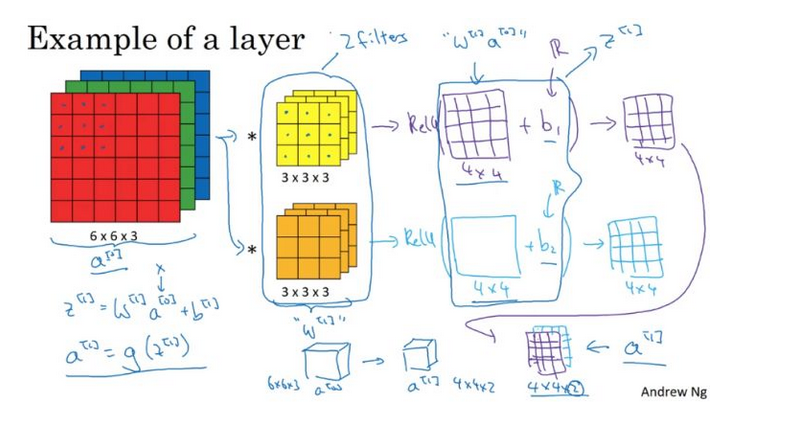
与普通神经网络单层前向传播类似，卷机神经网络也是先由权重和bias做线性运算，然后得到结果在输入到一个激活函数中。

对应上图a[0]表示图片层（nn3）

w[1]对应卷积核（ff3）

a[1] 对应下一层（4x4x2）

单层卷积参数个数

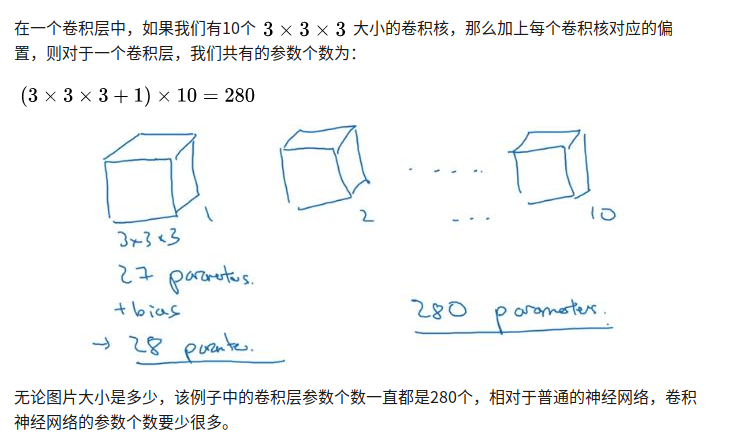
不受图片大小影响

标记

f[l] 卷积核大小

卷积核第三个维度大小等于输入图片通道数

而权重就是卷积核大小×卷积核个数，卷积核个数就是输出层的通道数目

激活值大小就是下一层输出层的大小： nH X nW X nC

简单卷积网络

最后得到的7x7x40，一共1960个参数，就是最后输入激活函数的所有参数

池化层

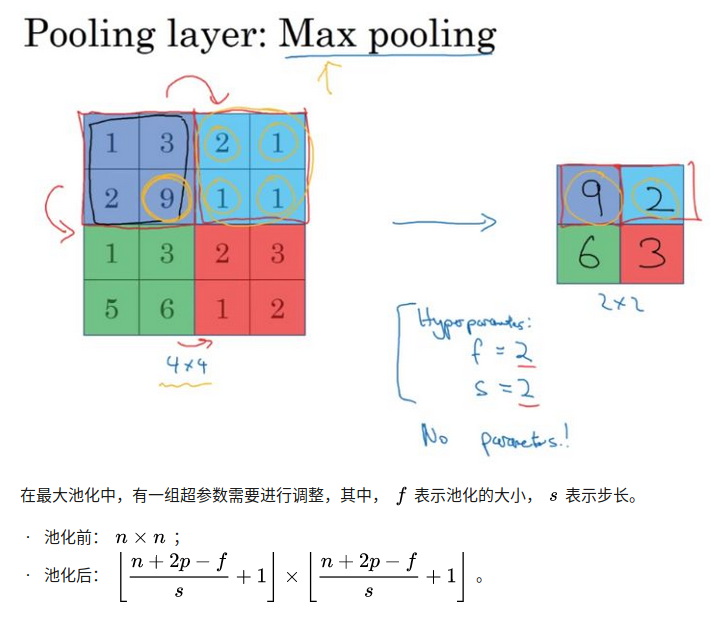
最大池化(max pooling)

把前一层得到的特征图进行池化减小，仅由当前小区域内的最大值来代表最终池化后的值。

平均池化

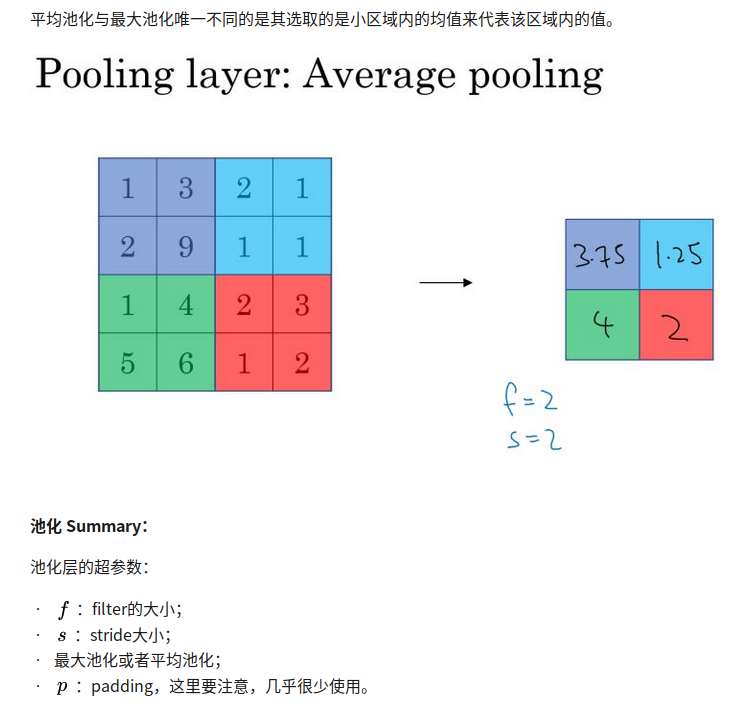
池化只需要设置好超参数，没有要学习的参数

总结

CNN的最大特点在于卷积的权值共享结构，可以大幅减少神经网络参数量，防止过拟合的同时又降低了神经网络模型的复杂度。

CNN通过卷积的方式实现局部链接，得到图片的参数量只跟卷积核的大小有关，一个卷积核对应一个图片特征，每一个卷积核滤波得到的图像就是一类特征的映射。

也就是说训练的权值数量只与卷积核大小与数量有关，但注意的是隐含层节点数量没有下降，隐含节点的数量只与卷积的步长有关，如果步长为1，那么隐含节点数量与输入图像像素数量一致。如果步长为5，那么每5x5个像素才需要一个隐含节点。

再总结，CNN的要点就是

1.局部连接

2.权值共享

3.池化层的降采样

其中1与2降低了参数量，训练复杂度下降并减轻过拟合。

同时权值共享赋予了卷积网络对平移的容忍性。

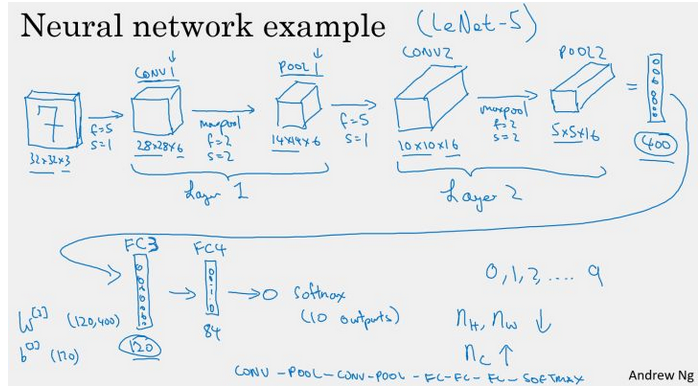
随着nn层数增加，提取的特征图片大小将会减小，但是同时间通道数量会增加

为什么使用CNN？

1.参数少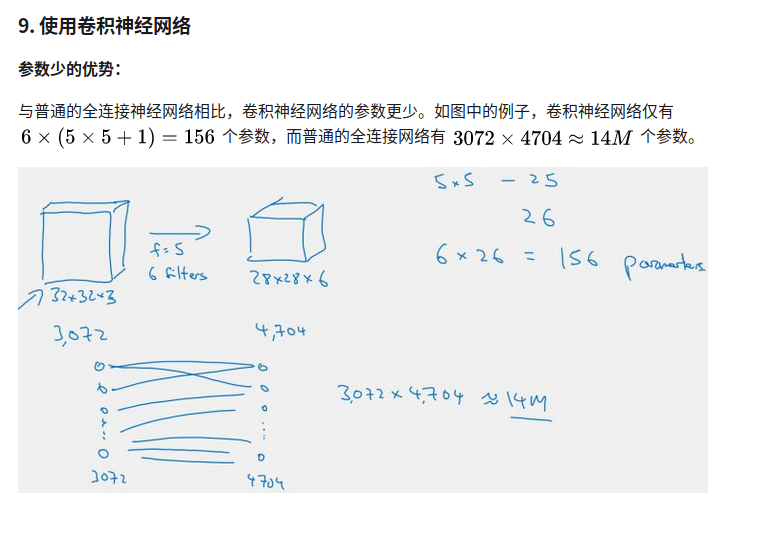

2.参数共享&链接的稀疏性

参数共享指一个卷积核可以有多个不同的卷积核，而每一个卷积核对应一个滤波后映射出的新图像，同一个新图像的每一个像素都来自完全相同的卷积核。

implementation

zero padding

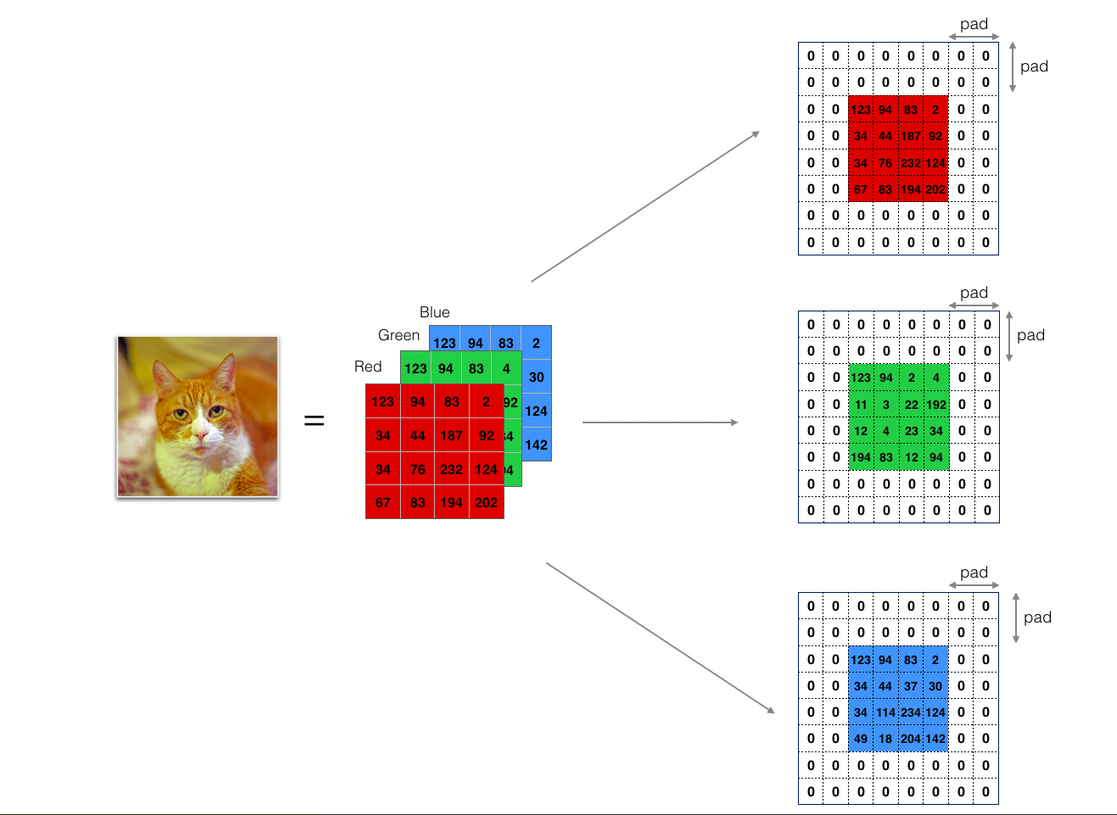
benefits

def zero_pad(X, pad):
    """
    Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image, 
    as illustrated in Figure 1.
    
    Argument:
    X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
    pad -- integer, amount of padding around each image on vertical and horizontal dimensions
    
    Returns:
    X_pad -- padded image of shape (m, n_H + 2*pad, n_W + 2*pad, n_C)
    """
    
    ### START CODE HERE ### (≈ 1 line)
    X_pad = np.pad(X, ((0, 0), (pad, pad), (pad, pad), (0, 0)), 'constant', constant_values=0)
    ### END CODE HERE ###
    
    return X_pad

forward convolution

def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.
    
    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
    
    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """

    ### START CODE HERE ### (≈ 2 lines of code)
    # Element-wise product between a_slice and W. Add bias.
    s = np.multiply(a_slice_prev, W) + b
    # Sum over all entries of the volume s
    Z = np.sum(s)
    ### END CODE HERE ###

    return Z

define a slice

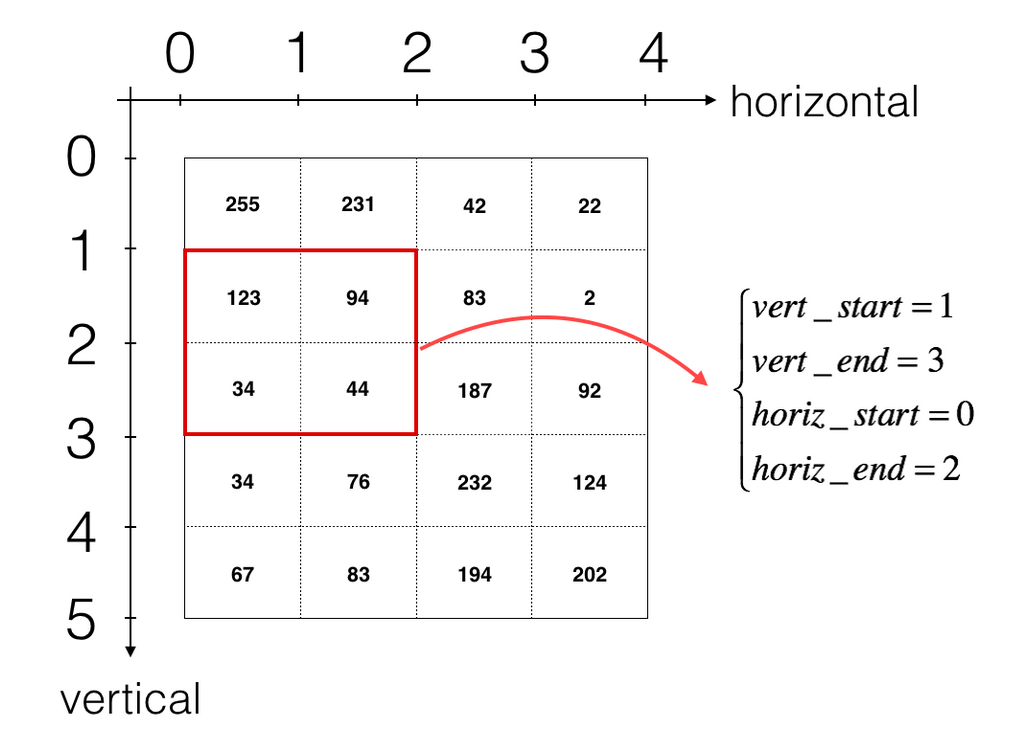
def conv_forward(A_prev, W, b, hparameters):
    """
    Implements the forward propagation for a convolution function
    
    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
    b -- Biases, numpy array of shape (1, 1, 1, n_C)
    hparameters -- python dictionary containing "stride" and "pad"
        
    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from A_prev's shape (≈1 line)  
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve dimensions from W's shape (≈1 line)
    (f, f, n_C_prev, n_C) = W.shape

    # Retrieve information from "hparameters" (≈2 lines)
    stride = hparameters['stride']
    pad = hparameters['pad']
    
    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)
    n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
    n_W = int((n_W_prev - f + 2 * pad) / stride) + 1
    
    # Initialize the output volume Z with zeros. (≈1 line)
    Z = np.zeros((m, n_H, n_W, n_C))
    
    # Create A_prev_pad by padding A_prev
    A_prev_pad = zero_pad(A_prev, pad)
    
    for i in range(m):                                 # loop over the batch of training examples
        a_prev_pad = A_prev_pad[i]                     # Select ith training example's padded activation
        for h in range(n_H):                           # loop over vertical axis of the output volume
            for w in range(n_W):                       # loop over horizontal axis of the output volume
                for c in range(n_C):                   # loop over channels (= #filters) of the output volume
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h * stride
                    vert_end = vert_start + f
                    horiz_start = w * stride
                    horiz_end = horiz_start + f
                    # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
                    a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)
                    Z[i, h, w, c] = conv_single_step(a_slice_prev, W[...,c], b[...,c])
                                        
    ### END CODE HERE ###

    # Making sure your output shape is correct
    assert(Z.shape == (m, n_H, n_W, n_C))
    
    # Save information in "cache" for the backprop
    cache = (A_prev, W, b, hparameters)
    
    return Z, cache

对应的notebook

https://github.com/AlexanderChiuluvB/deep-learning-coursera/blob/master/Convolutional%20Neural%20Networks/Convolution%20model%20-%20Step%20by%20Step%20-%20v1.ipynb