DL C2wk1

Posted on

Train/dev/test sets

dev sets,also called hold-out sets, are used to decide the model’s performance.(give you an unbiased estimate of your model’s performance)

example:

If you have 10,000,000 examples, how would you split the train/dev/test set?

98% train . 1% dev . 1% test

The dev and test set should:

Come from the same distribution

Bias and Variance

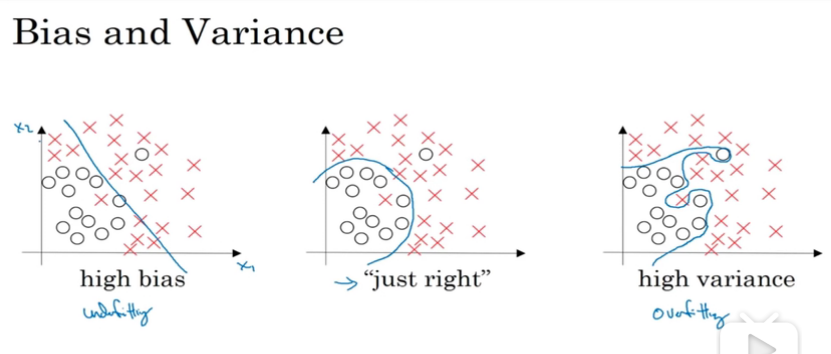
upload succesul

underfitting -> high bias

overfitting -> high variance

example

filename aady exists, renamed

1.如果train error =1%,dev set error = 11%

则overfitting，说明是high variance

2.如果 train error都很大的话，说明是high bias

3.总的来说，如果dev set error 比train set error
大很多，可以说明是overfitting

high bias and high variance

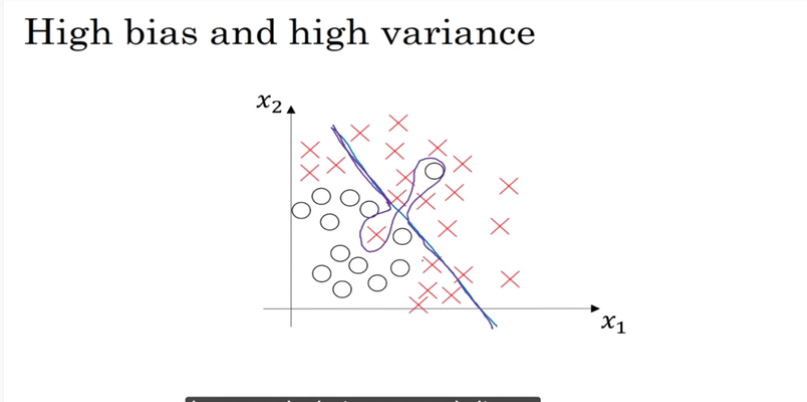
upload essful

部分数据过拟合，部分欠拟合

basic recipe for ML

如果high bias咋办

High bias （欠拟合）
(training data performance)

  • 1.bigger network
  • 2.optimized neural network architecture
  • 3.other optimizing techniques

High Variance? （过拟合）
(dev data performance)

  • 1.more data
  • 2.regularization

Regularization

filename alrea exists, renamed

在L1正则化中,w会是一个很sparse的向量，通常在实际应用中L2正则化会应用的更为广泛。

λ 又叫正则化参数

推导

filename alrea exists, renamed

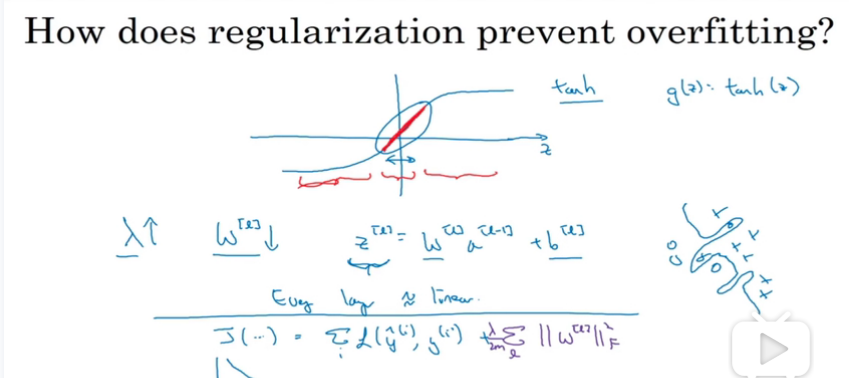
how does it work?

由上面推导我们可知，如果λ越大，那么w会越接近于0，那么以下图的激活函数为例，如果z很小的时候，tanh结果会接近于线性的，，神经网络每一层都将近似于一个线性神经元，那么就可以有效解决过拟合问题，往”欠拟合”或者刚好的方向。

upload successful

drop out

let’s say a nn with layer l = 3,keep_prob = 0.8

1
d3= np.random.rand(a3.shape[0],a3.shape[1])<keep_prob

80%的unit会被保留，20%会被drop out

上面语句作用是d380%元素为1,20%元素为0

1
a3 = np.multiply(a3,d3)

然后再scale up

1
a3/= keep_prob

why does it work?

upload succeful

1.在一些神经元很多的层，设置keep_probs低一点，可以有效减少过拟合，实际上是减弱regularization 的作用，在一些神经元很少的层，设置为1.0就好

2.在CV领域，由于输入数据的维数通常很大，一般都需要drop out

3.但是drop out会导致不能够通过画出cost function曲线来debug，解决方法是最开始先把所有keep_prob set to 1,then if no bug, turn on drop out

other technique of reducing overfitting

early stopping

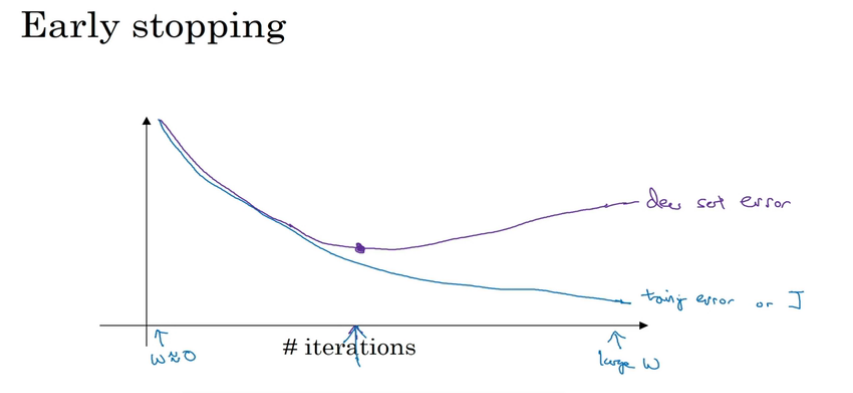
filena already exists, renamed

防止dev set error增加，采取early stopping,最后会得到一个middle-size的||w||^2

data augmentation

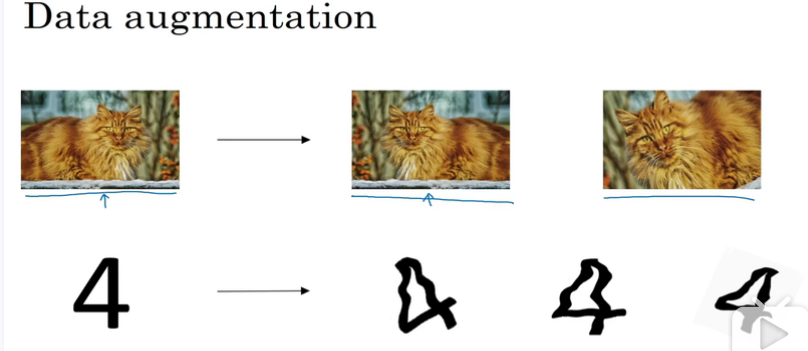
filename alre exists, renamed

通过变换现有的数据集，来获得更多的数据集

normalizing inputs

filename alrea exists, renamed

by subtract the mean and scalling the variance

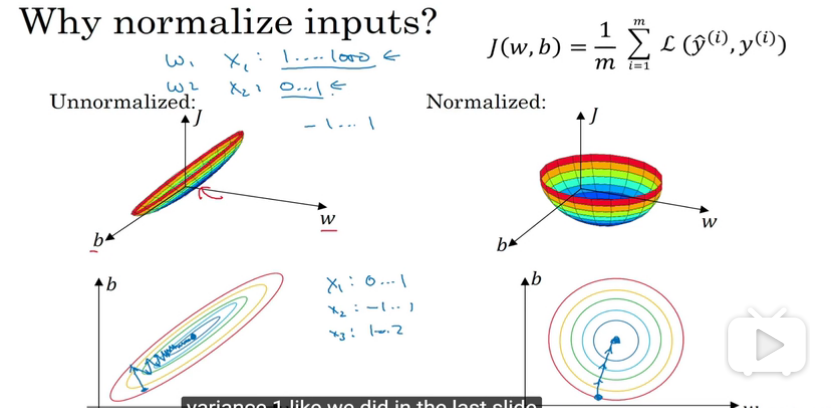
filename exists, renamed

效果就是会加快optimizing 的速度

Vanishing gradients

很深层的神经网络，权重相乘累积起来的话后果很严重

filename already exists, renmed

参数初始化方法：

这样可以使得w的值接近于1，不会导致梯度消失和梯度爆炸

upload cessful

其中的Xavior initialization

可以用来保证输入输出数据的分布相近，加快收敛速度（方差与均值大概相同）

https://blog.csdn.net/shuzfan/article/details/51338178

gradient checking

upload ccessful

grad check

upload essful

notes

1.no use in training ,only to debug

2.if fails grad check,look at components to try to identify bug.

3.remember regularization

4.doesn’t work with dropout

5.run at random initialization

initialization

zero initialization

如果把W矩阵初始化为0的话，相当于在训练一个各层只有一个神经元的神经网络，因为每一层的每个神经元其实都在学习相同的参数。

这时候神经网络只相当于一个线性分类器。

但是bias可以设置处值为0

large random initialization

1.poor initialization can lead to vanishing/exploding gradients

2.如果一开始w初值非常大，梯度下降所花时间会很长，（需要更多迭代次数）

He random initialization

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
     
    for l in range(1, L + 1):
        ### START CODE HERE ### (≈ 2 lines of code)
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * (np.sqrt(2. / layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
        ### END CODE HERE ###
        
    return parameters

xavier random initialization

只是把 sqrt（2./layers_dims[l-1]） 换作sqrt（1./layers_dims[l-1]）

L2 Regularization

flename already exists, renamed

同时code如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def compute_cost_with_regularization(A3, Y, parameters, lambd):
    """
    Implement the cost function with L2 regularization. See formula (2) above.
    
    Arguments:
    A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    parameters -- python dictionary containing parameters of the model
    
    Returns:
    cost - value of the regularized loss function (formula (2))
    """
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]
    
    cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
    
    ### START CODE HERE ### (approx. 1 line)
    sumW1 = np.sum(np.square(W1))
    sumW2 = np.sum(np.square(W2))
    sumW3 = np.sum(np.square(W3))
    L2_regularization_cost = (0.5/m*lambd)*(sumW1+sumW2+sumW3)
    ### END CODER HERE ###
    
    cost = cross_entropy_cost + L2_regularization_cost
    
    return cost

同时引入正则化的话，在backword propa的时候，要加上正则项

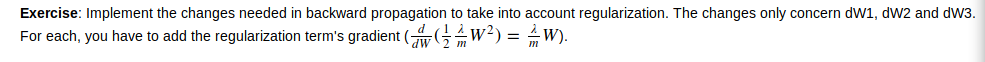
upload sussful

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def backward_propagation_with_regularization(X, Y, cache, lambd):
    """
    Implements the backward propagation of our baseline model to which we added an L2 regularization.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation()
    lambd -- regularization hyperparameter, scalar
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    
    ### START CODE HERE ### (approx. 1 line)
    dW3 = 1./m * np.dot(dZ3, A2.T) + (lambd/m)*W3
    ### END CODE HERE ###
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    ### START CODE HERE ### (approx. 1 line)
    dW2 = 1./m * np.dot(dZ2, A1.T) + (lambd/m)*W2
    ### END CODE HERE ###
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    ### START CODE HERE ### (approx. 1 line)
    dW1 = 1./m * np.dot(dZ1, X.T) + (lambd/m)*W1
    ### END CODE HERE ###
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

lambd = 0.6

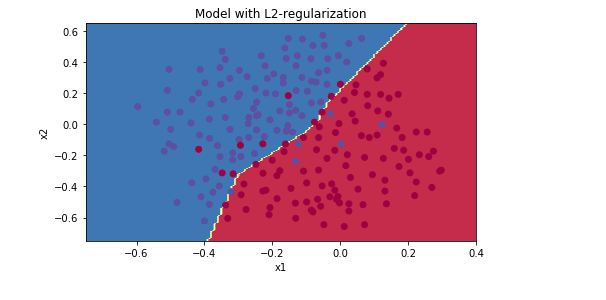
filename al exists, renamed

lambd = 0.7

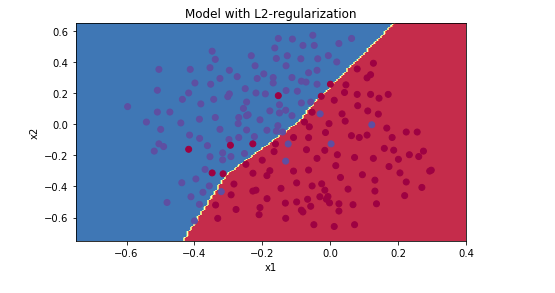
upload succsful

lambd = 0.8

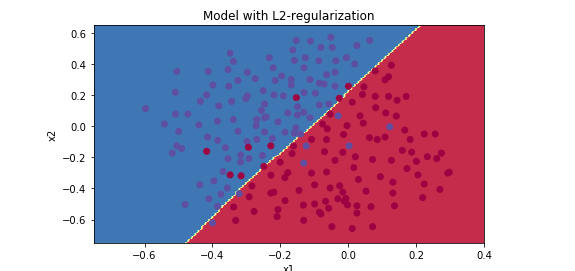
filename already exists,amed

λ增大，能够减少过拟合现象，但是training set error 也会随之减少

drop out

what is inverted dropout?

upload cessful

upload ful

drop out

upload successul

1.创建一个np.array D1 which has the same size as A1（np.random.randn(A.shape[0],A.shape[1])）

2.当A的元素<D[keep_prob]的时候为1，大于的时候为0

3.A = np.multiply(A,D)

4.scale A,i.e. A/=keep_prob (inverted dropout)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
    """
    Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape (20, 2)
                    b1 -- bias vector of shape (20, 1)
                    W2 -- weight matrix of shape (3, 20)
                    b2 -- bias vector of shape (3, 1)
                    W3 -- weight matrix of shape (1, 3)
                    b3 -- bias vector of shape (1, 1)
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    A3 -- last activation value, output of the forward propagation, of shape (1,1)
    cache -- tuple, information stored for computing the backward propagation
    """
    
    np.random.seed(1)
    
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    ### START CODE HERE ### (approx. 4 lines)         # Steps 1-4 below correspond to the Steps 1-4 described above. 
    D1 = np.random.rand(A1.shape[0], A1.shape[1])     # Step 1: initialize matrix D1 = np.random.rand(..., ...)
    D1 = D1 < keep_prob                            # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
    A1 = A1 * D1                                      # Step 3: shut down some neurons of A1
    A1 = A1 / keep_prob                               # Step 4: scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    ### START CODE HERE ### (approx. 4 lines)
    D2 = np.random.rand(A2.shape[0], A2.shape[1])     # Step 1: initialize matrix D2 = np.random.rand(..., ...)
    D2 = D2 < keep_prob                           # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)                           
    A2 = A2 * D2                                      # Step 3: shut down some neurons of A2
    A2 = A2 / keep_prob                               # Step 4: scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)
    
    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
    
    return A3, cache

drop out in backward

just perform dA2*=D2 and scaling

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
    """
    Implements the backward propagation of our baseline model to which we added dropout.
    
    Arguments:
    X -- input dataset, of shape (2, number of examples)
    Y -- "true" labels vector, of shape (output size, number of examples)
    cache -- cache output from forward_propagation_with_dropout()
    keep_prob - probability of keeping a neuron active during drop-out, scalar
    
    Returns:
    gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
    """
    
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1. / m * np.dot(dZ3, A2.T)
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
    dA2 = np.dot(W3.T, dZ3)
    ### START CODE HERE ### (≈ 2 lines of code)
    dA2 = dA2 * D2              # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
    dA2 = dA2 / keep_prob              # Step 2: Scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1. / m * np.dot(dZ2, A1.T)
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
    
    dA1 = np.dot(W2.T, dZ2)
    ### START CODE HERE ### (≈ 2 lines of code)
    dA1 = dA1 * D1              # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
    dA1 = dA1 / keep_prob              # Step 2: Scale the value of neurons that haven't been shut down
    ### END CODE HERE ###
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, 
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

gradient checking

以J = x*theta 为例

upload succesul

implementation

upload succeful

注意

1
np.linalg.norm 是求范数的函数，默认是求二范数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def gradient_check(x, theta, epsilon = 1e-7):
    """
    Implement the backward propagation presented in Figure 1.
    
    Arguments:
    x -- a real-valued input
    theta -- our parameter, a real number as well
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.
    ### START CODE HERE ### (approx. 5 lines)
    thetaPlus = theta+epsilon
    thetaMinus = theta-epsilon
    JPlus = forward_propagation(x,thetaPlus)
    JMinus = forward_propagation(x,thetaMinus)
    gradapprox = (JPlus-JMinus)/(2*epsilon)
    ### END CODE HERE ###
    
    # Check if gradapprox is close enough to the output of backward_propagation()
    ### START CODE HERE ### (approx. 1 line)
    grad = backward_propagation(x, gradapprox)
    ### END CODE HERE ###
        
    ### START CODE HERE ### (approx. 1 line)
    numerator = np.linalg.norm(grad-gradapprox)
    demurator = np.linalg.norm(grad)+np.linalg.norm(gradapprox)
    difference = numerator/demurator
    
    
    if difference < 1e-7:
        print ("The gradient is correct!")
    else:
        print ("The gradient is wrong!")
    
    return difference

对于多维的情况

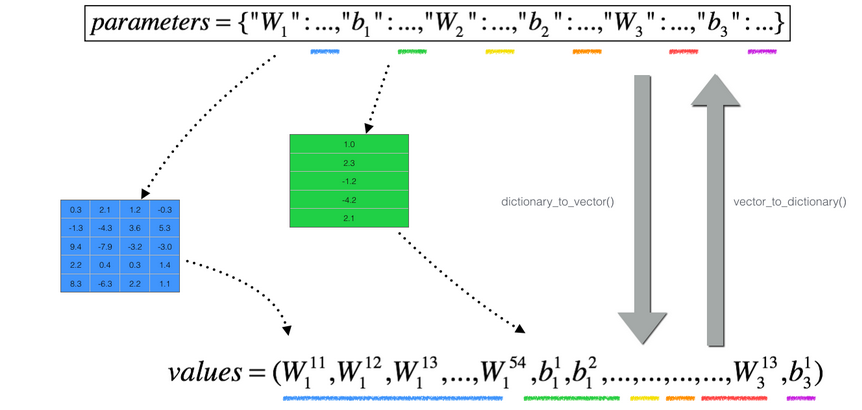
upload success

把所有params压缩到一个向量，然后一个for循环，计算每个参数的grad，gradapprox，并加入到一个向量当中，分别得到一个gradapprox与grad向量，再利用这两个向量求范数，求difference

filename already exists, reamed

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
    """
    Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
    
    Arguments:
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
    grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 
    x -- input datapoint, of shape (input size, 1)
    y -- true "label"
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    # Compute gradapprox
    for i in range(num_parameters):
        
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        # "_" is used because the function you have to outputs two parameters but we only care about the first one
        ### START CODE HERE ### (approx. 3 lines)
        thetaplus =  np.copy(parameters_values)                                       # Step 1
        thetaplus[i][0] = thetaplus[i][0] + epsilon                                   # Step 2
        J_plus[i], _ =  forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))  # Step 3
        ### END CODE HERE ###
        
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        ### START CODE HERE ### (approx. 3 lines)
        thetaminus = np.copy(parameters_values)                                       # Step 1
        thetaminus[i][0] = thetaminus[i][0] - epsilon                                 # Step 2        
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus)) # Step 3
        ### END CODE HERE ###
        
        # Compute gradapprox[i]
        ### START CODE HERE ### (approx. 1 line)
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
        ### END CODE HERE ###
    
    # Compare gradapprox to backward propagation gradients by computing difference.
    ### START CODE HERE ### (approx. 1 line)
    numerator = np.linalg.norm(grad - gradapprox)                                     # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)                   # Step 2'
    difference = numerator / denominator                                              # Step 3'
    ### END CODE HERE ###

    if difference > 1e-7:
        print("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
    else:
        print("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference

concolusion

1.L2正则化和drop out都可以帮你解决overfitting

2.regularization 会使得weight变得非常小