DL C2wk2

Posted on | In

mini batch gradient descent

mini-batch size

  • if mini-batch size = m （m=sample size）

(X^[i],Y^[i]) = (X,Y)

收敛速度会很快（步长很大）

end up with batch gradient descent,which has to process the whole training set before making progress

  • mini-batch size = 1 又叫做stocastic gradient descent

收敛步长会很小，很有可能会不收敛，而且vectorization会很慢

lose the benefits of vectorization

如下图

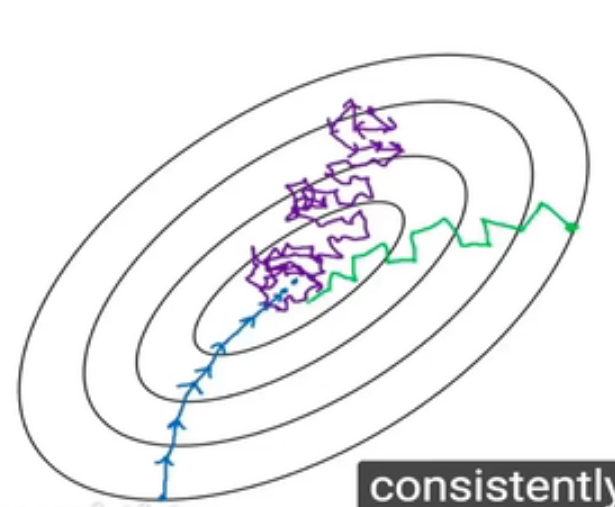
filename alrea exists, renamed

紫色表示batch size=1的收敛，而蓝色表示batch size=m的收敛。

how to choose mini-batch size?

1.通常用 64,128,256,512大小(power of two)

upload sucsful

upload sessful

upload ssful

learning rate decay

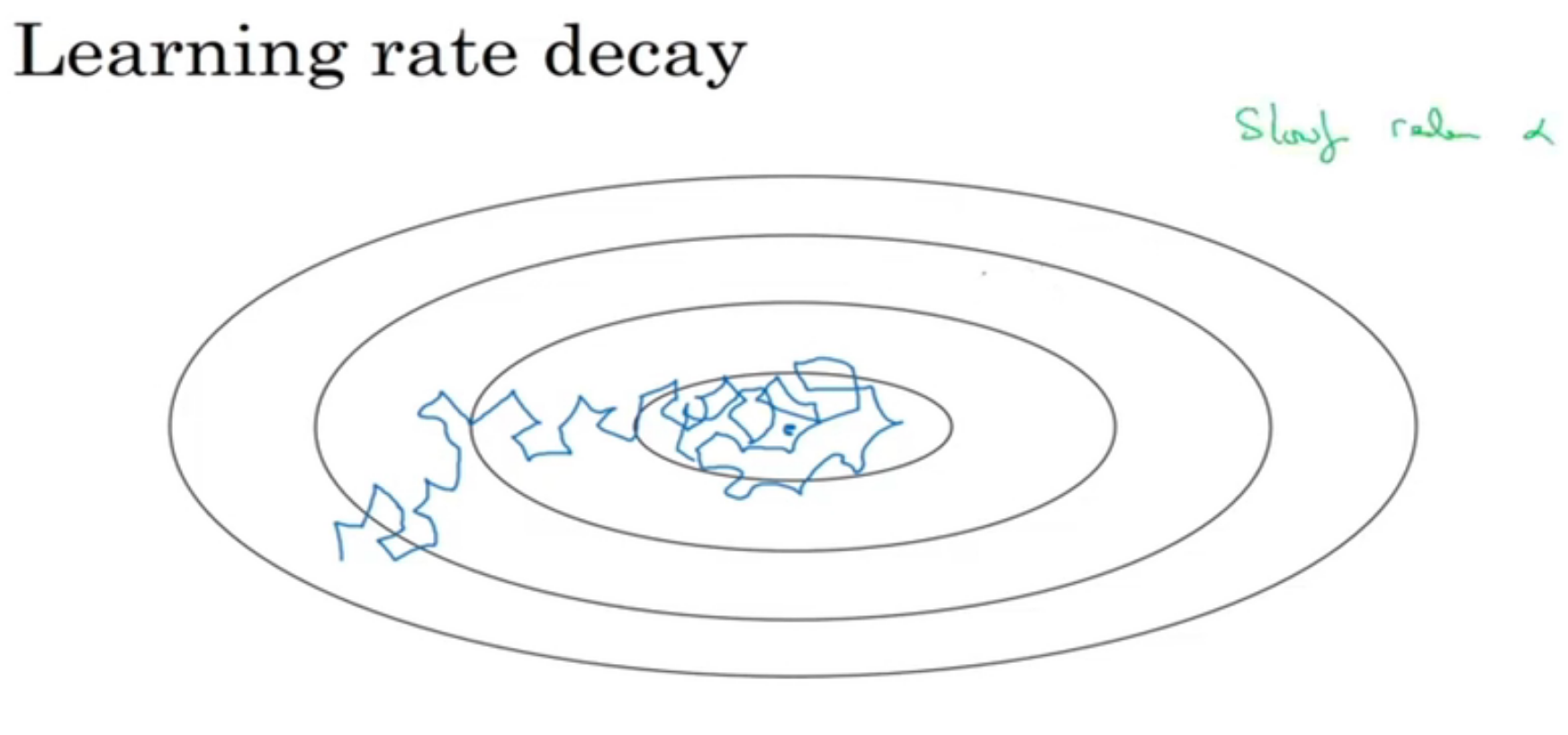
upload essful

当梯度下降的时候，由于学习率是固定的，因此可能会在最低点附近徘徊而最终不能收敛。

implementation

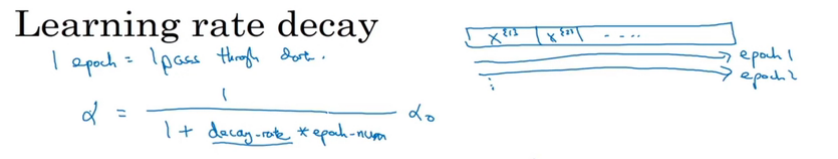
upload essful

alpha = 1/（1+decay_rate x epoch_num） *alpha

其他方法也可：

upload succeful

mini-Batch gradient descent

shuffle

upload sful

parition

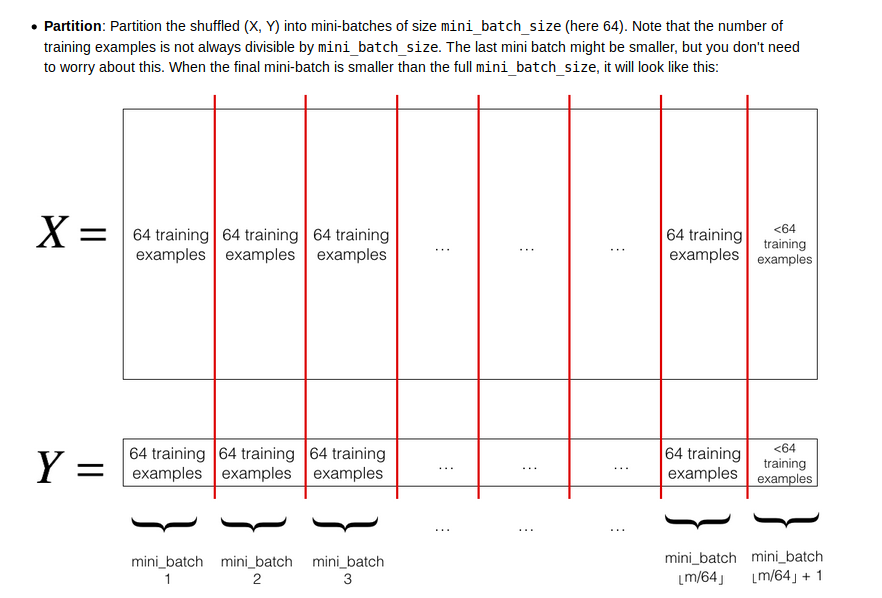
load successful

code

注意最后一个batch_size有可能和前面的size不同，因为样本总数可能不等于batch_size的倍数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
    Creates a list of random minibatches from (X, Y)
    
    Arguments:
    X -- input data, of shape (input size, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
    mini_batch_size -- size of the mini-batches, integer
    
    Returns:
    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
    """
    
    np.random.seed(seed)            # To make your "random" minibatches the same as ours
    m = X.shape[1]                  # number of training examples
    mini_batches = []
        
    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1,m))

    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        ### START CODE HERE ### (approx. 2 lines)
        mini_batch_X = shuffled_X[:,mini_batch_size*(k):mini_batch_size*(k+1)]
        mini_batch_Y = shuffled_Y[:,mini_batch_size*(k):mini_batch_size*(k+1)]
        ### END CODE HERE ###
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        ### START CODE HERE ### (approx. 2 lines)
        mini_batch_X = shuffled_X[:,mini_batch_size*(num_complete_minibatches):]
        mini_batch_Y = shuffled_Y[:,mini_batch_size*(num_complete_minibatches):]
        ### END CODE HERE ###
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
    
    return mini_batches

momentum

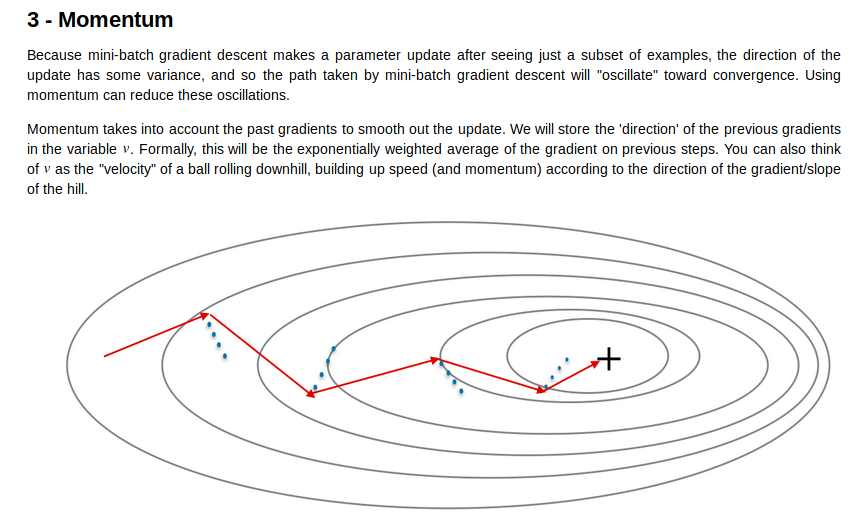
filename already exists, named

蓝色是gradient的方向，而红色是实际velocity的方向，我们让gradient影响velocty下降的方向

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def initialize_velocity(parameters):
    """
    Initializes the velocity as a python dictionary with:
                - keys: "dW1", "db1", ..., "dWL", "dbL" 
                - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    
    Returns:
    v -- python dictionary containing the current velocity.
                    v['dW' + str(l)] = velocity of dWl
                    v['db' + str(l)] = velocity of dbl
    """
    
    L = len(parameters) // 2 # number of layers in the neural networks
    v = {}
    
    # Initialize velocity
    for l in range(L):
        ### START CODE HERE ### (approx. 2 lines)
        v["dW" + str(l+1)] = np.zeros(parameters['W'+str(l+1)].shape)
        v["db" + str(l+1)] = np.zeros(parameters['b'+str(l+1)].shape)
        ### END CODE HERE ###
        
    return v

update parameters

filename already exists, remed

upload succesul

Adam optimization

upload succeul

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def initialize_adam(parameters) :
    """
    Initializes v and s as two python dictionaries with:
                - keys: "dW1", "db1", ..., "dWL", "dbL" 
                - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
    
    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters["W" + str(l)] = Wl
                    parameters["b" + str(l)] = bl
    
    Returns: 
    v -- python dictionary that will contain the exponentially weighted average of the gradient.
                    v["dW" + str(l)] = ...
                    v["db" + str(l)] = ...
    s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                    s["dW" + str(l)] = ...
                    s["db" + str(l)] = ...

    """
    
    L = len(parameters) // 2 # number of layers in the neural networks
    v = {}
    s = {}
    
    # Initialize v, s. Input: "parameters". Outputs: "v, s".
    for l in range(L):
    ### START CODE HERE ### (approx. 4 lines)
        v["dW" + str(l+1)] = np.zeros_like(parameters['W'+str(l+1)]) #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
        v["db" + str(l+1)] = np.zeros_like(parameters['b'+str(l+1)]) #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])
        s["dW" + str(l+1)] = np.zeros_like(parameters['W'+str(l+1)]) #(numpy array of zeros with the same shape as parameters["W" + str(l+1)])
        s["db" + str(l+1)] = np.zeros_like(parameters['b'+str(l+1)]) #(numpy array of zeros with the same shape as parameters["b" + str(l+1)])


    ### END CODE HERE ###
    
    return v, s

update parameters

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01,
                                beta1=0.9, beta2=0.999, epsilon=1e-8):
    """
    Update parameters using Adam
    
    Arguments:
    parameters -- python dictionary containing your parameters:
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    grads -- python dictionary containing your gradients for each parameters:
                    grads['dW' + str(l)] = dWl
                    grads['db' + str(l)] = dbl
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    learning_rate -- the learning rate, scalar.
    beta1 -- Exponential decay hyperparameter for the first moment estimates 
    beta2 -- Exponential decay hyperparameter for the second moment estimates 
    epsilon -- hyperparameter preventing division by zero in Adam updates

    Returns:
    parameters -- python dictionary containing your updated parameters 
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    """
    
    L = len(parameters) // 2                 # number of layers in the neural networks
    v_corrected = {}                         # Initializing first moment estimate, python dictionary
    s_corrected = {}                         # Initializing second moment estimate, python dictionary
    
    # Perform Adam update on all parameters
    for l in range(L):
        # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
        ### START CODE HERE ### (approx. 2 lines)
        v['dW'+str(l+1)] = beta1*v['dW'+str(l+1)]+(1-beta1)*grads['dW'+str(l+1)]
        v['db'+str(l+1)] = beta1*v['db'+str(l+1)]+(1-beta1)*grads['db'+str(l+1)]
        ### END CODE HERE ###

        # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        v_corrected['dW'+str(l+1)] = v['dW'+str(l+1)]/(1-np.power(beta1,t))
        v_corrected['db'+str(l+1)] = v['db'+str(l+1)]/(1-np.power(beta1,t))
        ### END CODE HERE ###

        # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
        ### START CODE HERE ### (approx. 2 lines)
        s['dW'+str(l+1)] = beta2*s['dW'+str(l+1)]+(1-beta2)*np.power(grads['dW'+str(l+1)],2)
        s['db'+str(l+1)] = beta2*s['db'+str(l+1)]+(1-beta2)*np.power(grads['db'+str(l+1)],2)
        ### END CODE HERE ###

        # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        s_corrected['dW'+str(l+1)] = s['dW'+str(l+1)]/(1-np.power(beta2,t))
        s_corrected['db'+str(l+1)] = s['db'+str(l+1)]/(1-np.power(beta2,t))
        ### END CODE HERE ###

        # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
        ### START CODE HERE ### (approx. 2 lines)
        parameters['W'+str(l+1)] -= learning_rate * v_corrected['dW'+str(l+1)] /(epsilon+np.sqrt(s_corrected['dW'+str(l+1)]))
        parameters['b'+str(l+1)] -= learning_rate * v_corrected['db'+str(l+1)] /(epsilon+np.sqrt(s_corrected['db'+str(l+1)]))
        
        ### END CODE HERE ###

    return parameters, v, s

usage

注意每次epoch的时候，分为多个batch学习参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0.9,
          beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True):
    """
    3-layer neural network model which can be run in different optimizer modes.
    
    Arguments:
    X -- input data, of shape (2, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
    layers_dims -- python list, containing the size of each layer
    learning_rate -- the learning rate, scalar.
    mini_batch_size -- the size of a mini batch
    beta -- Momentum hyperparameter
    beta1 -- Exponential decay hyperparameter for the past gradients estimates 
    beta2 -- Exponential decay hyperparameter for the past squared gradients estimates 
    epsilon -- hyperparameter preventing division by zero in Adam updates
    num_epochs -- number of epochs
    print_cost -- True to print the cost every 1000 epochs

    Returns:
    parameters -- python dictionary containing your updated parameters 
    """

    L = len(layers_dims)             # number of layers in the neural networks
    costs = []                       # to keep track of the cost
    t = 0                            # initializing the counter required for Adam update
    seed = 10                        # For grading purposes, so that your "random" minibatches are the same as ours
    
    # Initialize parameters
    parameters = initialize_parameters(layers_dims)

    # Initialize the optimizer
    if optimizer == "gd":
        pass # no initialization required for gradient descent
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)
    
    # Optimization loop
    for i in range(num_epochs):
        
        # Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
        seed = seed + 1
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        for minibatch in minibatches:

            # Select a minibatch
            (minibatch_X, minibatch_Y) = minibatch

            # Forward propagation
            a3, caches = forward_propagation(minibatch_X, parameters)

            # Compute cost
            cost = compute_cost(a3, minibatch_Y)

            # Backward propagation
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)

            # Update parameters
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
            elif optimizer == "adam":
                t = t + 1 # Adam counter
                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
                                                               t, learning_rate, beta1, beta2,  epsilon)
        
        # Print the cost every 1000 epoch
        if print_cost and i % 1000 == 0:
            print("Cost after epoch %i: %f" % (i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
                
    # plot the cost
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters