PRML-线性模型

Posted on

线性基函数模型

线性回归模型 y(x,w) = w0+w1x1+w2x2+…wDxD

而为了改进模型，把xi替换为非线性表达式

uploaccessful

本实验使用了多项式基函数，高斯基函数和sigmoid基函数，以及混合型（多项式+sin正弦）而损失函数有两种选择，交叉熵函数以及均方误差，这里选择均方误差，求导比较方便。

推导

多项式基函数

y = w0+w1x1+w2x2^2 + b

λ2是L2正则化系数，可以解决过拟合问题

正则化意义：https://blog.csdn.net/jinping_shi/article/details/52433975

推导

filename alrey exists, renamed

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

import numpy as np

def propogate(w,b,X,Y):

    """
    :param w: (n,1)
    :param b: scalar
    :param X: (n,m)
    :param Y: (1,n)
    :return: grads a dict that saves the params dw,db
            cost saves the cost after each iteration
    """
    #np.squeeze
    #squeeze 函数：从数组的形状中删除单维度条目，即把shape中为1的维度去掉
    m = X.shape[1]

    Yba = np.dot(w.T,X) + b

    cost = np.squeeze((0.5/m *np.dot((Yba-Y),(Yba-Y).T)))

    dw = (1./m) * np.dot(X,(Yba-Y).T)

    db = (1./m) * np.squeeze(np.sum(Yba-Y))
    #save the updated result to the grads dict
    grads = {"dw":dw,"db":db}

    return grads,cost

def optimize(w,b,X,Y,epochs,learning_rate,l2):
    """
    
    :param w: (n,1) 
    :param b: scalar
    :param X: (n,m)
    :param Y: (1,n)
    :param epochs: 迭代次数 
    :param learning_rate: 
    :param l2: 正则化系数 
    :return: params
            grads save the final params ,used for test
            costs save the cost
    """

    costs = []

    for i in range(epochs):
        grads,cost = propogate(w,b,X,Y)
        dw = grads["dw"]
        db = grads["db"]

        w-=learning_rate*dw+l2*w
        b-=learning_rate*db

    params = {"w":w,"b":b}
    grads = {"dw":dw,"db":db}

    return params,grads,costs

def main(x_train, y_train,n,epoches,learning_rate,l2):
    """训练模型，并返回从x到y的映射。"""

    # 使用线性回归训练模型，根据训练集计算最优化参数
    ## 请补全此处代码，替换以下示例
    m = x_train.shape[0]
    w = (np.random.randn(n,1))
    X = np.zeros((n,m),dtype = np.float64)
    b = np.float(0)
    for i in range(n):
        X[i,:] = x_train**(i+1)
    Y = np.float64(np.reshape(y_train,newshape=(1,m)))
    params,grads,costs = optimize(w,b,X,Y,epoches,learning_rate,l2)
    w = params['w']
    b = params['b']
    def f(x):
        ## 请补全此处代码，替换以下示例
        m = x.shape[0]

        X = np.zeros((n,m))
        for i in range(n):
            X[i,:] = x**(i+1)
        y = b+np.dot(w.T,X)
        return y.squeeze()
        pass

    return f

result

参数：n=2 epochs = 100000 lr 1e-7

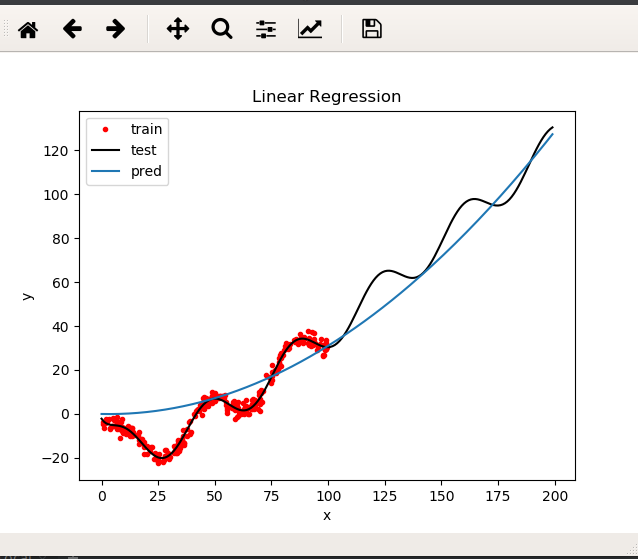
filename alrey exists, renamed

高斯基函数

upload succeful

推导

upload ssful

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
import numpy as np

def propogate(w,b,X,Y,mu,s):

    m = X.shape[1]
    Z = (X-mu)/s
    A = np.exp(-(Z*Z)/2)
    Yba = np.dot(w.T,A) + b
    cost = np.squeeze((0.5/m *np.dot((Yba-Y),(Yba-Y).T)))

    dY = 1./m*(Yba-Y)
    dw = np.dot(A,dY.T)
    db = np.squeeze(np.sum(dY))
    dA = w*dY
    dZ = dA*A*(-Z)
    dmu = 1./m*np.sum(dZ*(-1/s),axis=1,keepdims=True)
    ds = 1./m*np.sum(dZ*(-(X-mu)/(s*s)),axis=1,keepdims=True)


    grads = {"dw":dw,"db":db,"dmu":dmu,"ds":ds}

    return grads,cost


def optimize(w,b,X,Y,mu,s,epochs,learning_rate,l2):

    costs = []

    for i in range(epochs):
        grads,cost = propogate(w,b,X,Y,mu,s)
        dw = grads["dw"]
        db = grads["db"]
        dmu = grads["dmu"]
        ds = grads["ds"]

        w-=learning_rate*dw+l2*w
        b-=learning_rate*db+l2*b
        mu-=learning_rate*dmu+l2*mu
        s -=learning_rate*ds+l2*s

        costs.append(cost)

    params = {"w":w,"b":b,"mu":mu,"s":s}


    return params,costs



def main(x_train, y_train,n,epoches,learning_rate,l2):
    """训练模型，并返回从x到y的映射。"""

    # 使用线性回归训练模型，根据训练集计算最优化参数
    ## 请补全此处代码，替换以下示例
    m = x_train.shape[0]
    w = (np.random.randn(n,1))
    # means of gaussian
    mu = np.random.randn(n,1)
    #I still have no idea why set like this?
    for i in range(n):
        mu[i,0]+=i*40
    X = np.zeros((n,m),dtype = np.float64)
    b = np.float(0)
    for i in range(n):
        X[i,:] = x_train
    Y = np.float64(np.reshape(y_train,newshape=(1,m)))

    #initalize s if s is too close to 0 then it will go wrong
    while True:
        flag = True
        s = np.random.randn(n,1)
        jump = np.int32(np.abs(s)<1)
        if(np.sum(jump))>=1:
            flag = False
        if flag is True:
            break

    params,costs = optimize(w,b,X,Y,mu,s,epoches,learning_rate,l2)
    w = params['w']
    b = params['b']
    mu = params['mu']
    s = params['s']
    def f(x):
        ## 请补全此处代码，替换以下示例
        m = x.shape[0]

        X = np.zeros((n,m))
        for i in range(n):
            X[i,:] = x
        Z = (X-mu)/s
        A = np.exp(-(Z*Z)/2)
        y = b+np.dot(w.T,A)
        return y.squeeze()
        pass

    return f

参数：f = gaussian.main(x_train, y_train,3,500000,1e-2,0)

结果

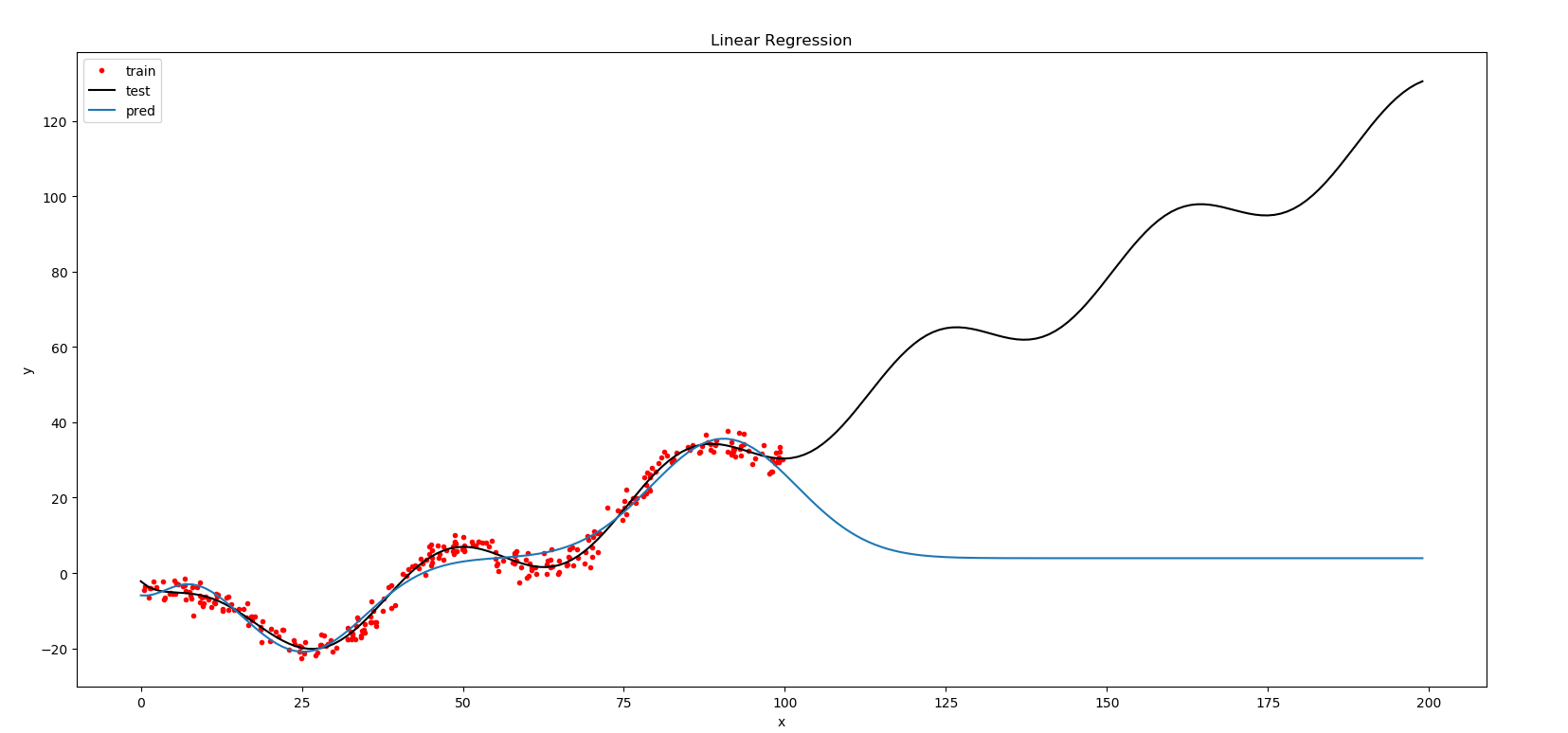
fileme already exists, renamed

sigmoid 函数

upload succeful

推导

结果与高斯类似

fiename already exists, renamed

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
import numpy as np

def sigmoidFunction(z):
    return 1./(1+np.exp(-z))


def propogate(w,b,X,Y,mu,s):

    m = X.shape[1]
    Z = (X-mu)/s
    A = sigmoidFunction(Z)
    Yba = np.dot(w.T,A) + b
    cost = np.squeeze((0.5/m *np.dot((Yba-Y),(Yba-Y).T)))

    dY = 1./m*(Yba-Y)
    dw = np.dot(A,dY.T)
    db = np.squeeze(np.sum(dY))
    dA = w*dY
    dZ = dA*A*(1-A)
    dmu = 1./m*np.sum(dZ*(-1./s),axis=1,keepdims=True)
    ds = 1./m*np.sum(dZ*(-(X-mu)/(s*s)),axis=1,keepdims=True)


    grads = {"dw":dw,"db":db,"dmu":dmu,"ds":ds}

    return grads,cost


def optimize(w,b,X,Y,mu,s,epochs,learning_rate,l2):



    costs = []

    for i in range(epochs):
        grads,cost = propogate(w,b,X,Y,mu,s)
        dw = grads["dw"]
        db = grads["db"]
        dmu = grads["dmu"]
        ds = grads["ds"]

        w-=learning_rate*dw+l2*w
        b-=learning_rate*db+l2*b
        mu-=learning_rate*dmu+l2*mu
        s -=learning_rate*ds+l2*s

        costs.append(cost)

    params = {"w":w,"b":b,"mu":mu,"s":s}


    return params,costs



def main(x_train, y_train,n,epoches,learning_rate,l2):
    """训练模型，并返回从x到y的映射。"""

    # 使用线性回归训练模型，根据训练集计算最优化参数
    ## 请补全此处代码，替换以下示例
    m = x_train.shape[0]
    w = (np.random.randn(n,1))
    # means of gaussian
    mu = np.random.randn(n,1)
    # mu is the mean of the sigmoid
    for i in range(n):
        mu[i,0]+= i*100/n
    X = np.zeros((n,m),dtype = np.float64)
    b = np.float(0)
    for i in range(n):
        X[i,:] = x_train
    Y = np.float64(np.reshape(y_train,newshape=(1,m)))

    #initalize s if s is too close to 0 then it will go wrong
    while True:
        flag = True
        s = np.random.randn(n,1)
        jump = np.int32(np.abs(s)<1)
        if(np.sum(jump))>=1:
            flag = False
        if flag is True:
            break

    params,costs = optimize(w,b,X,Y,mu,s,epoches,learning_rate,l2)
    w = params['w']
    b = params['b']
    mu = params['mu']
    s = params['s']
    def f(x):
        ## 请补全此处代码，替换以下示例
        m = x.shape[0]

        X = np.zeros((n,m))
        for i in range(n):
            X[i,:] = x
        Z = (X-mu)/s
        A = sigmoidFunction(Z)
        y = b+np.dot(w.T,A)
        return y.squeeze()
        pass

    return f

参数： f = sigmoid.main(x_train, y_train,10,100000,1e-2,0)

结果

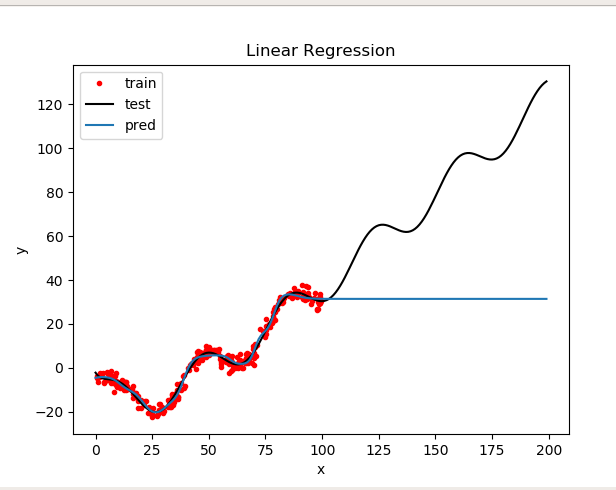
upload successful

reference

https://github.com/Haicang/PRML/blob/master/lab1/Report.ipynb

https://blog.csdn.net/pipisorry/article/details/73770637