DS-动态规划

Leetcode 647

Given an unsorted array of integers, find the length of longest continuous increasing subsequence (subarray).

Example 1:

Input: [1,3,5,4,7]
Output: 3
Explanation: The longest continuous increasing subsequence is [1,3,5], its length is 3.
Even though [1,3,5,7] is also an increasing subsequence, it’s not a continuous one where 5 and 7 are separated by 4.

int findLengthOfLCIS(vector<int>& nums) {
       if(nums.empty())
           return 0;
       int n = nums.size();
       int dp[n];
       dp[0]=1;
       int res = 1;
       for(int i=1;i<nums.size();i++){
           if(nums[i-1]<nums[i]){
               dp[i] = dp[i-1]+1;
           }
           else{
               dp[i] = 1;
           }
           res = max(dp[i],res);
       }
       return res;
   }

printLIS 路径

//M saves the index
int M[MAX+1];
int pre[MAX+1];
int pathIndex[MAX+1];

vector<int>vec;

void print(int pos){
    if(pos==-1)return;
    print(pre[pos]);
    cout<<" "<<vec[pos];
}

int main(){

    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    int N;
    while(true){
        cin>>N;
        if(N==0)
            break;
        vec.assign(N,0);
        for(int i=0;i<N;i++){
            cin>>vec[i];
        }
        int L = 0;
        for(int i=0;i<N;i++){
            int lo = 1;
            int Hi = L;
            //find the largest mid <=L such that vec[M[mid]]<vec[i]
            while(lo<=Hi){
                int mid = ceil((lo+Hi)/2.0);
                if(vec[M[mid]]<vec[i]){
                    lo=mid+1;
                }else{
                    Hi = mid-1;
                }
            }

            //newL is 1 greater than the longest prefix of vec[i]
            int newL = lo;
            //vec[i]的前驱节点是newL-1子串的最后一个索引
            pre[i] = M[newL-1];
			//NEWL新子串的最后一个索引就是i
            M[newL] = i;

            if(newL>L)
                L = newL;
        }

        int k = M[L];
        for(int i=L-1;i>=0;i--){
            pathIndex[i] = k;
            k = pre[k];
        }
        cout<<L<<" ";
        for(int i=0;i<=L-1;i++){
            cout<<vec[pathIndex[i]]<<" ";
        }
        cout<<endl;


    }

}

Leetcode 300

Given an unsorted array of integers, find the length of longest increasing subsequence.

Example:

Input: [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

int lengthOfLIS(vector<int>& nums) {
    
       if(nums.empty())
           return 0;
        int n = nums.size();
        int dp[n];
        for(int i=0;i<n;i++)
            dp[i]=1;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[j]<nums[i]){
                    //仅当dp[j]+1>dp[i]的时候才更新
                    if(dp[j]+1>dp[i]){
                        dp[i]=dp[j]+1;
                    }
                }
            }
        }
        int res = 0;
        for(int i=0;i<n;i++)
            res = max(res,dp[i]);
        return res;
    }

复杂度：O（n^2）

解析：

https://www.youtube.com/watch?v=CE2b_-XfVDk

以下是O(nlogn)作法

int lengthOfLIS(vector<int>& nums) {
    
       if(nums.empty())
           return 0;
        int n = nums.size();
        int dp[n];
        dp[0] = nums[0];
        int len=1;
        for(int i=1;i<n;i++){
            int left=0;
            int right = len-1;
            int mid;
            if(dp[len-1]<nums[i]){
                dp[len++]=nums[i];
            }else{
                while(left<=right){
                    mid = (left+right)/2;
                    if(dp[mid]<nums[i]){
                        left = mid+1;
                    }else{
                        right = mid-1;
                    }
                }
                dp[left] = nums[i];
            }
            
        }
        
        return len;
    }
};

dp[i]表示长度为i的LIS序列的最后一个数字最小末尾

https://www.cnblogs.com/ziyi--caolu/p/3227121.html

leetcode 53

Longest maximum subarray

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

int max_sum(vector<int>&nums,int i){
        if(i==0)
            return nums[i];
        int res = max(nums[i],nums[i]+max_sum(nums,i-1));
        return res;
    }
    
    int maxSubArray(vector<int>& nums) {
        
        if(nums.empty())
            return 0;
        int res = nums[0];
        for(int i=0;i<nums.size();i++){
            res = max(res,max_sum(nums,i));
        }
        return res;
        
        
    }

方法二：

转移方程： dp[i] = nums[i]+(dp[i-1]>0?dp[i-1]:0);

int maxSubArray(vector<int>& nums) {
      if(nums.empty())
          return 0;
      int n = nums.size();
      int dp[n];
      dp[0] = nums[0];
      int res = dp[0];
      for(int i=1;i<n;i++){
          dp[i] = nums[i]+(dp[i-1]>0?dp[i-1]:0);
          res = max(res,dp[i]);
      }
      return res;
  }

拓展

给定K个整数的序列{ N1, N2, …, NK }，其任意连续子序列可表示为{ Ni, Ni+1, …,
Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个，
例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和
为20。
在今年的数据结构考卷中，要求编写程序得到最大和，现在增加一个要求，即还需要输出该
子序列的第一个和最后一个元素。

http://acm.hdu.edu.cn/showproblem.php?pid=1231

#include <iostream>
#include <cstring>

using namespace std;
#define INF 0x3f3f3f3f
int A[30][30][30];

int main(){

    int k;

    while(true){
        long long int dp[10001];
        int arr[10001];
        cin>>k;
        if(k==0)
            break;
        int posFlag = 0;
        for(int i=1;i<=k;i++){
            scanf("%d",&arr[i]);
            if(arr[i]>=0)
                posFlag=1;
        }
        if(posFlag!=1){
            cout<<0<<" "<<arr[1]<<" "<<arr[k]<<endl;
        }
        else{
            double max = -INF;
            dp[1]=arr[1];
            int resulti=1;
            for(int i=1;i<=k;i++){
                //or dp[i] = max(dp[i-1]+arr[i],arr[i])
                dp[i] = arr[i]+(dp[i-1]>0?dp[i-1]:0);
                if(dp[i]>max){
                    max = dp[i];
                    resulti = i;
                }
            }
            double max2=0;
            int start=1;
            for(int i=resulti;i>=1;i--){
                max2+=arr[i];
                if(max2==max){
                    start = i;
                    break;
                }
            }
            cout<<max<<" "<<arr[start]<<" "<<arr[resulti]<<endl;
        }

    }

}

关键是要找到子序列的第一个元素。

当找到最后一个元素的索引时候，从索引处由后往前找，知道sum等于结果的max，记录下此时的索引i，于是便找到了第一个元素的索引i

Longest common subsequence

转移方程 ： res = max(lcs(i-1,j),lcs(i,j-1),1+lcs(i-1,j-1))

string a="bananinn";
string b = "kaninan";

int lcs(int i,int j){
    if(i==-1||j==-1)
        return 0;


    int res=0;
    res = max(res,lcs(i-1,j));
    res = max(res,lcs(i,j-1));

    if(a[i]==b[j]){
        res = max(res,1+lcs(i-1,j-1));
    }
    return res;
}

int main(){
    int mem[1000][1000];
    memset(mem,-1,sizeof(mem));
    int ans = 0;
    for(int i=0;i<8;i++){
        for(int j=0;j<7;j++){
            ans = max(ans,lcs(i,j));
        }
    }
    cout<<ans<<endl;
}

DP模板

Dynamic programming formulation
map<problem, value> memory;
	value dp(problem P) {
		if (is_base_case(P)) {
			return base_case_value(P);
	}
		if (memory.find(P) != memory.end()) {
			return memory[P];
	}
		value result = some value;
		for (problem Q in subproblems(P)) {
			result = combine(result, dp(Q));	
		}
		memory[P] = result;
		return result;
}

Traveling Salesman problem

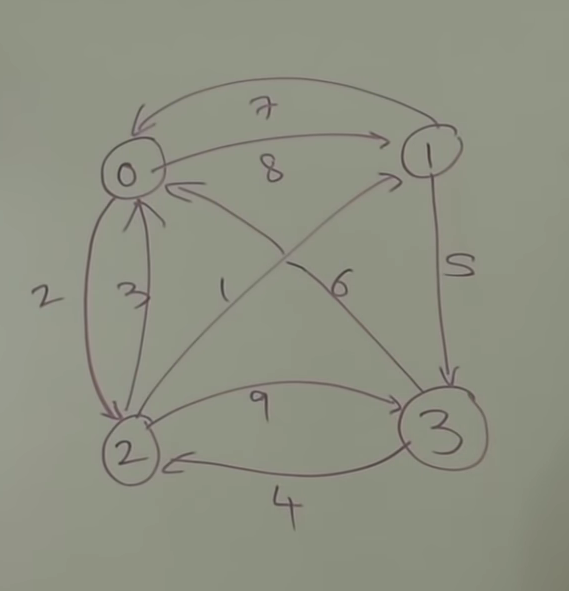
TSP问题就是在一张有权图，从某个起点出发，然后go through each node exactly once and finally return to the beginning node,such that the weightSum is minimal

NP-HARD

no solution with dominomial time complexity

子问题一共有 2^n*n 个，每个子问题用O(n)复杂度来解决

T:(2^n*n^2)

0-1背包问题

状态转移方程：

//f[i][j]表示i个物品，容量j背包的物品最大价值
//若f[i][j] == f[i-1][j],说明不装第i个
//否则装入第i个，同时容量-w,价值+v,w,v分别为第i个物品的重量和价值

f[i][j] = max(f[i-1][j],f[i-1][j-w]+v);

kattis - knapsack

关键是如何打印出装入的物品的index

int main(){
    double capa;
    int n;
    while(cin>>capa&&cin>>n){
        int capacity = floor(capa);
        vector<vector<int>>f(n+1,vector<int>(capacity+1,0));
        values.assign(n+1,0);
        weights.assign(n+1,0);
        for(int i=1;i<=n;i++){
            int v,w;
            cin>>v>>w;
            weights[i] = w;
            values[i] = v;
        }

        for(int i=1;i<=n;i++){
            int v = values[i];
            int w = weights[i];
            for(int j=1;j<=capacity;j++){
                if(j<w){
                    f[i][j] = f[i-1][j];
                    continue;
                }
                f[i][j] = max(f[i-1][j],f[i-1][j-w]+v);
            }
        }

        //打印最终装入的物品的index！ 即寻找f[i][j]!=f[i-1][j]
        vector<int>res;
        int j = capacity;
        for(int i=n;i>=1;i--){
            if(f[i][j]!=f[i-1][j]){
                res.push_back(i-1);
                j-=weights[i];
            }
        }
        cout<<res.size()<<endl;
        for(auto i:res)
            cout<<i<<" ";
        cout<<endl;
    }
}

http://poj.org/problem?id=1579

记忆化搜索

把递归结果存在表里，减少不必要的递归次数

int A[30][30][30];

int w(int a,int b,int c){
    if(a<=0||b<=0||c<=0){
        return 1;
    }
    if(a>20||b>20||c>20){
        return w(20,20,20);
    }
    if(A[a][b][c])  //if already in A no need to do recursion
        return A[a][b][c];
    if(a<b&&b<c){
        A[a][b][c] =w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c); //A[a][b][c-1]+A[a][b-1][c-1]-A[a][b-1][c];
    }
    else
        A[a][b][c] = w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);//A[a-1][b][c]+A[a-1][b-1][c]+A[a-1][b][c-1]-A[a-1][b-1][c-1];
    return A[a][b][c];
}

int main(){

    memset(A,0,sizeof(A));
    while(true){
        int a,b,c;
        cin>>a>>b>>c;
        if(a==-1&&b==-1&&c==-1)
            break;
        cout<<w(a,b,c)<<endl;
    }
    
}

dfs solve TSP

https://open.kattis.com/problems/beepers

dfs解TSP问题

基本思路是从出发点开始，尝试从出发点到其他所有点的可能性，然后回溯。

dfs的大概思路就是当n<num的时候，尝试到不同的点，回溯，当n==num的时候，比较现在的路径长度是否小于最短路径。

int shortest,num;
int startx,starty;
struct node{
    int x;
    int y;
};
vector<node>vec;
int visited[MAX];

int dis(int x1,int y1,int x2,int y2){
    return abs(x1-x2)+abs(y1-y2);
}

void DFS(int cur,int len,int n){

    if(n==num){
        int t = dis(vec[cur].x,vec[cur].y,startx,starty);
        if(len+t<shortest){
            shortest = len+t;
        }
    }else if(len<shortest){
        int i;
        for(i=0;i<num;i++){
            if(visited[i]==0){
                visited[i] = 1;
                DFS(i,len+dis(vec[cur].x,vec[cur].y,vec[i].x,vec[i].y),n+1);
                visited[i] = 0;
            }
        }
    }


}


int main(){

    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);


    int sc;
    int row,col;
    cin>>sc;
    while(sc--){
        cin>>row>>col;
        cin>>startx>>starty;
        cin>>num;
        vec.clear();
        for(int i=0;i<num;i++){
            int xx,yy;
            cin>>xx>>yy;
            vec.push_back({xx,yy});
        }
        shortest = INF;
        memset(visited,0,sizeof(visited));

        for(int i=0;i<num;i++){
            int tempL = dis(vec[i].x,vec[i].y,startx,starty);
            visited[i] = 1;
            DFS(i,tempL,1);
            visited[i] = 0;
        }
        cout<<shortest<<endl;
    }
}

leetcode 931

minimum falling path sum

int minFallingPathSum(vector<vector<int>>& A) {
    int res = INT_MAX;
    int row = A.size();
    int col = A[0].size();
    int dp[row][col+2];
   
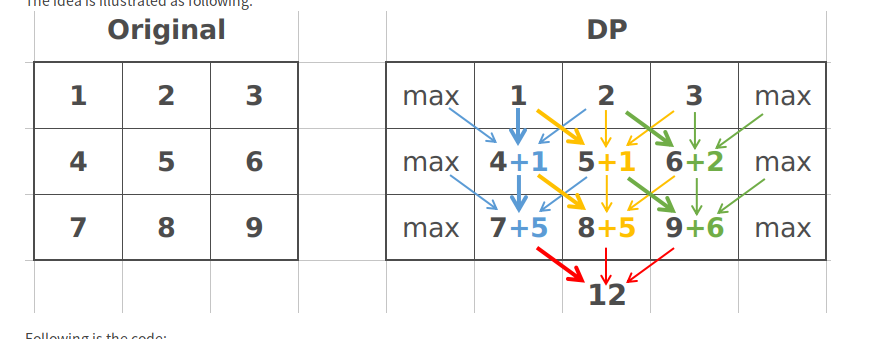
    for(int i=1;i<row;i++){
        for(int j=0;j<col;j++){
            if(j==0){
                A[i][j] = A[i][j]+min(A[i-1][j],A[i-1][j+1]);
            }
            else if(j==col-1){
                A[i][j] = A[i][j]+min(A[i-1][j],A[i-1][j-1]);
            }
            else
               A[i][j] = A[i][j]+min(A[i-1][j],min(A[i-1][j-1],A[i-1][j+1]));
        }
    }
    
    for(int i=0;i<col;i++){
        res = min(res,A[row-1][i]);
    }
    return res;
    
}

复杂度 n^2