DS-Topo,Bipartite,max flow&min cut

Posted on

Topological Sort

ver1 DFS

1
2
3
4
5
6
7
8
code:
for each unvisited node u in V:
	DFS(u)
    for each neighbour h of u:
    	if(!visited)
        	DFS(h)
    finish DFS(u) // push_back u to the list
reverse the list!

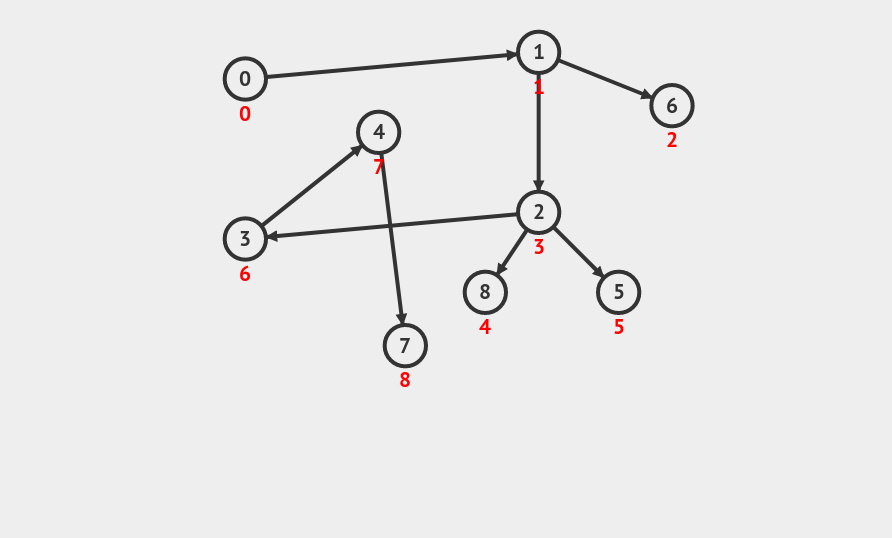
upload successl

ver2 BFS (Khan)

1
2
3
4
5
6
7
8
9
code:
push vertices with no incoming edges to the queue
while(!q.empty):
	u = q.top 
    q.pop
    for each neighbor x of u
    	delete u->x
        if x has no incoming edges,then push x to the queu
//done

Bipartite

definition

upload successfl

1.说白了就是图的所有点可以分为两个set，每个set之间互相没有边，只有set与set之间的点有边。

2.应用于无向图。

Bipartite checker

ver1 DFS

每个点的邻居与它不同色（就是不同一个set）

每个点与它的邻居的邻居同色，它邻居的邻居与它在同一个set

1
2
3
4
5
6
7
8
for each unvisited vertex in u:
	dfs(u)
    for each neighbor v in u:
    	if(v is unvisited)
        	assign u as different color
        else if u and v has same color
        	break!
            it is not a bipartite

ver2 BFS

1
2
3
4
5
6
7
8
9
push vertexs with no incoming edged to queue
while(!queue.empty())
	u = queue.top
    q.pop
    for v in neighbor in u
    	if(v.color==u.color)
        	exit;//no bipartite
        else if unvisited 
        	assign different color to v

max flow

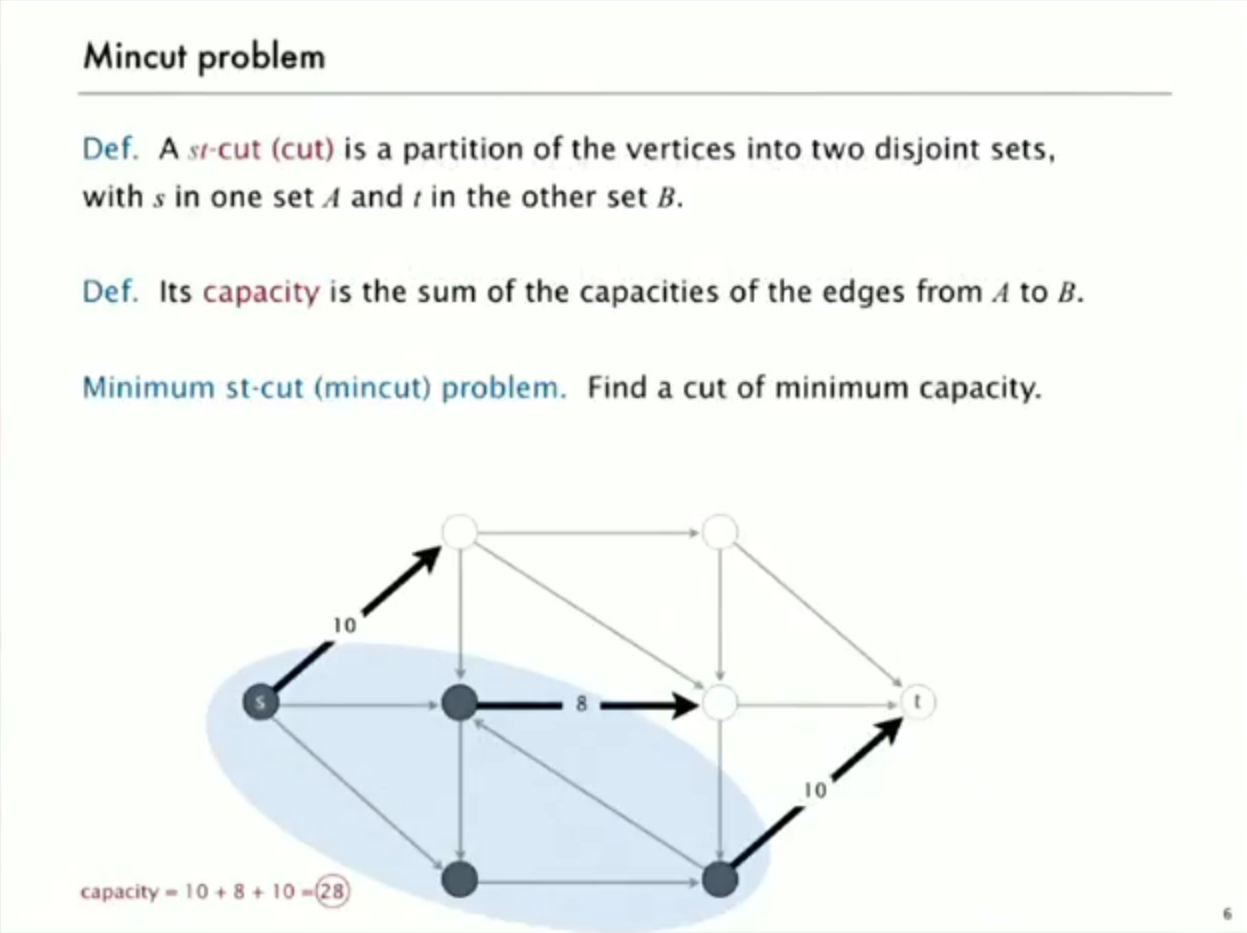
intro to mincut problem

filename already exists, renmed

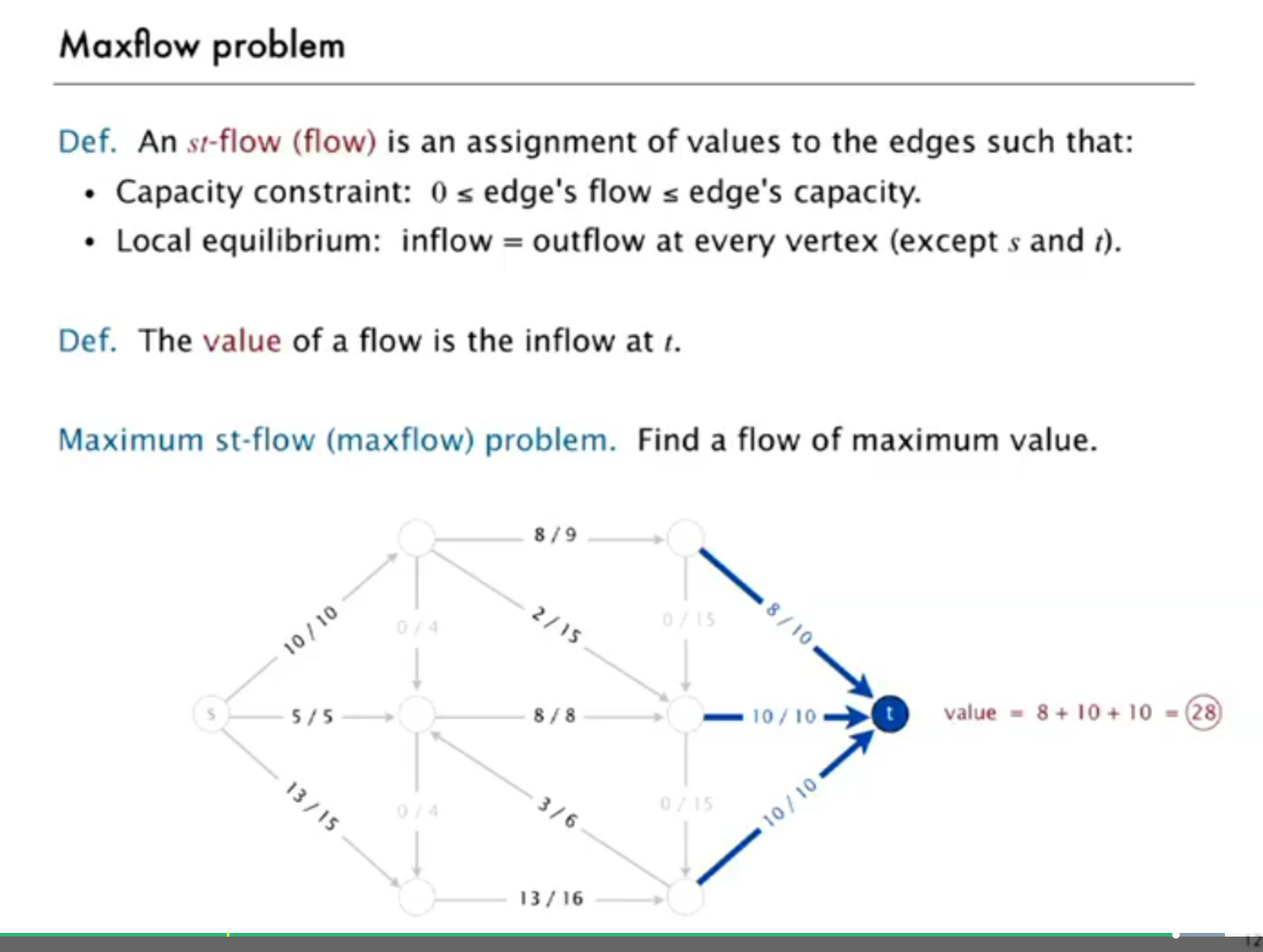
intro to maxflow problem

filename already exists, rename

Ford-Fulkerson Algorithm

mincut 和 maxflow problem 实际上是等价的，解决了其中一个，另外一个就自然解决了。

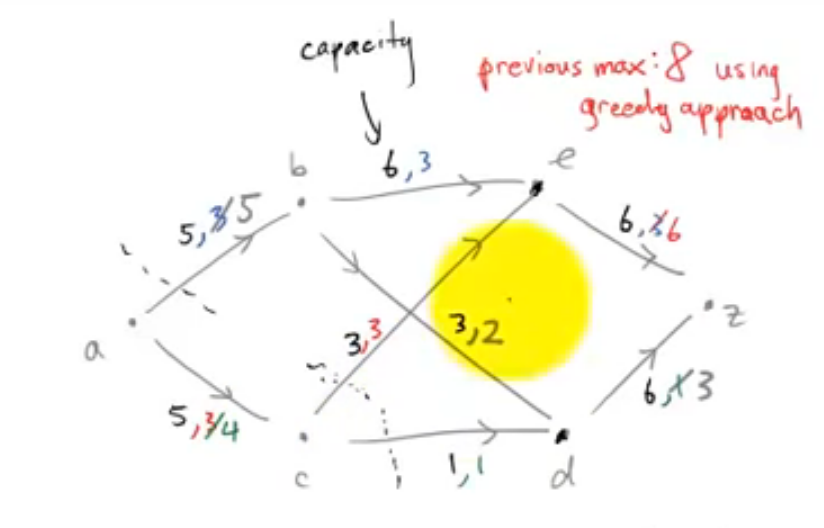
filename already exists, reamed

如上图，a为开始点。各边左数字为capacity，右边数字为flow

a->b满了，a->b有一个cut

a->c不满，即（flow<capacity）

c->e满了（flow==capacity）

c->d满了（flow==capacity）

设点a,c为集合P，其余所有点为集合P‘

则capacity of P->P’ 就等于maximum flow

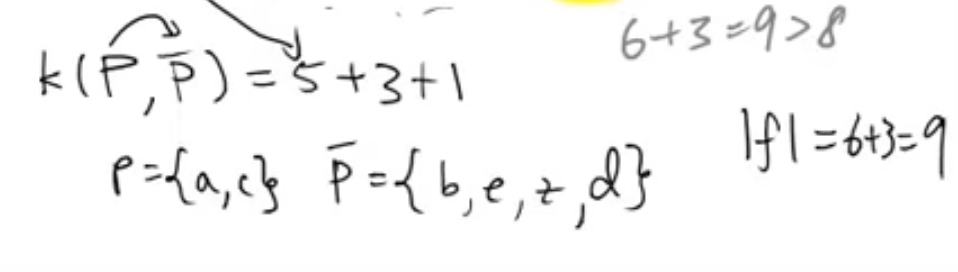
filename already exists, renaed

1
2
3
4
5
Start with 0 flow
while there exists an augmenting path:
	find an augmenting path
    compute bottleneck capacity
    increase flow on that path by bottleneck 	 capacity
Augmenting Path:

find an undirected path from s to t such that:

can increase flow on forward edges(not full.)
can decrease flow on backward edge(not empty.)
termination

all paths from s to t are blocked by either a:

full forward edge

empty backward edge

relationship between flow and cuts

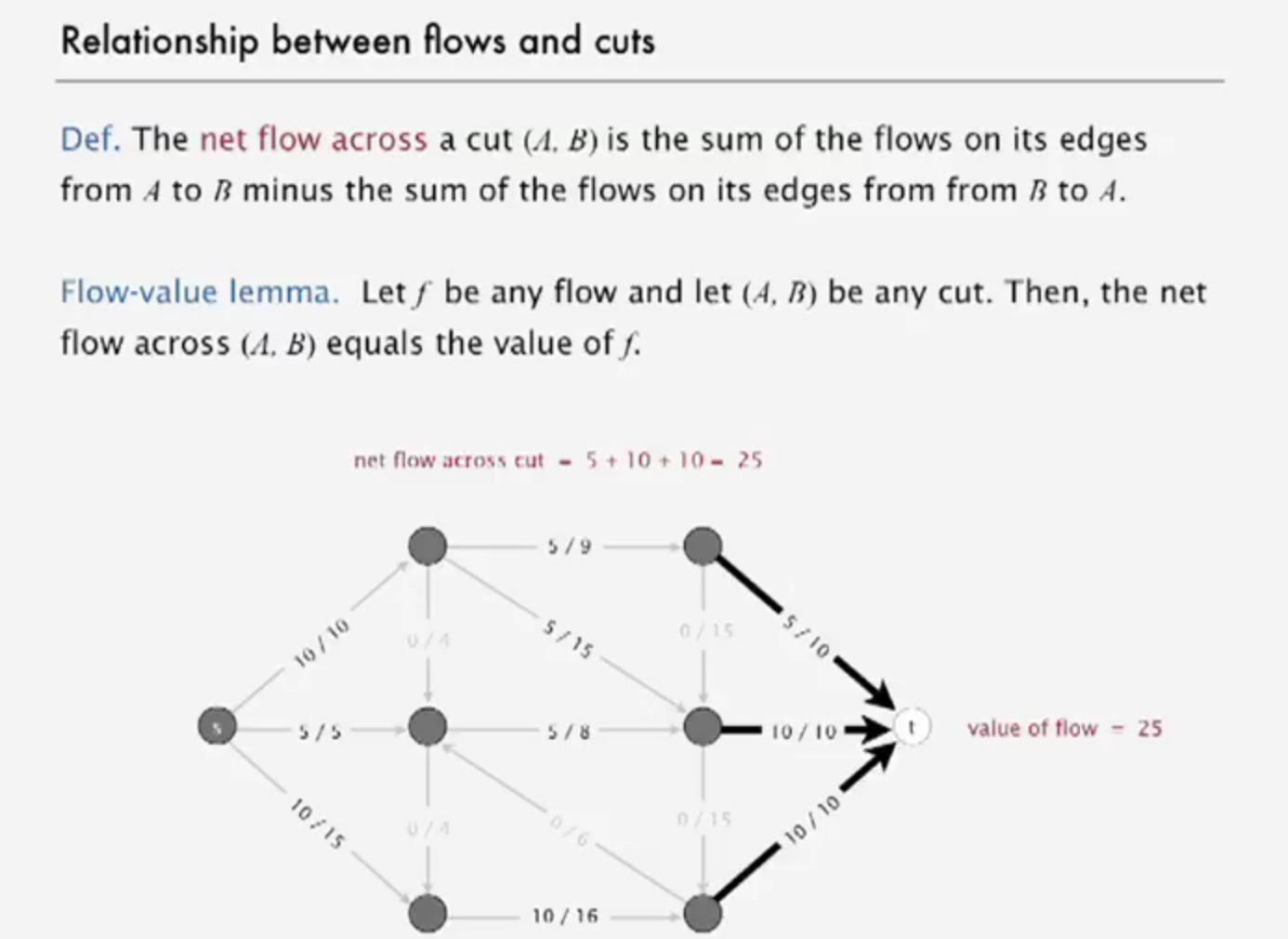
upload succesful

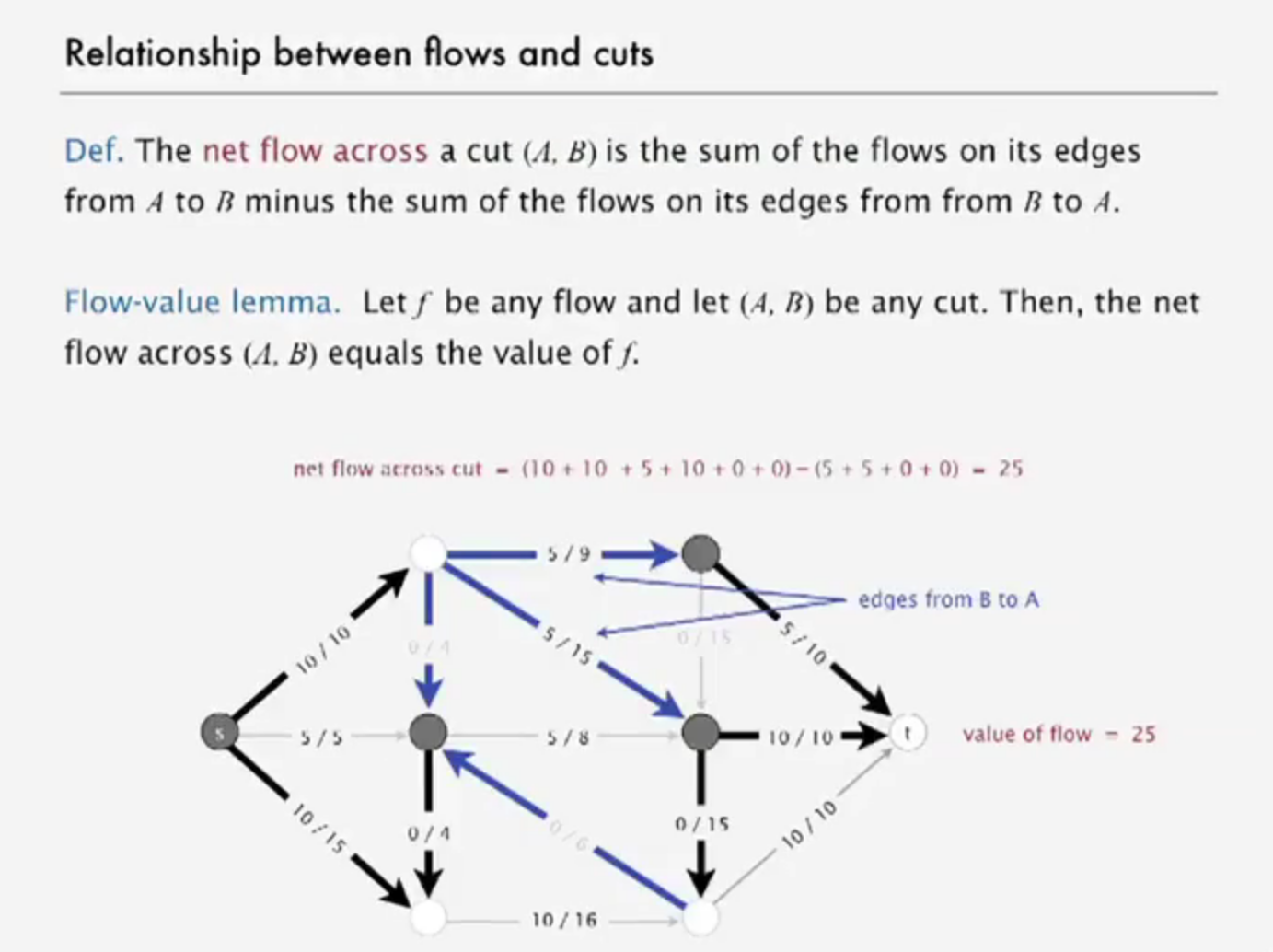
upload succsful

network of flow

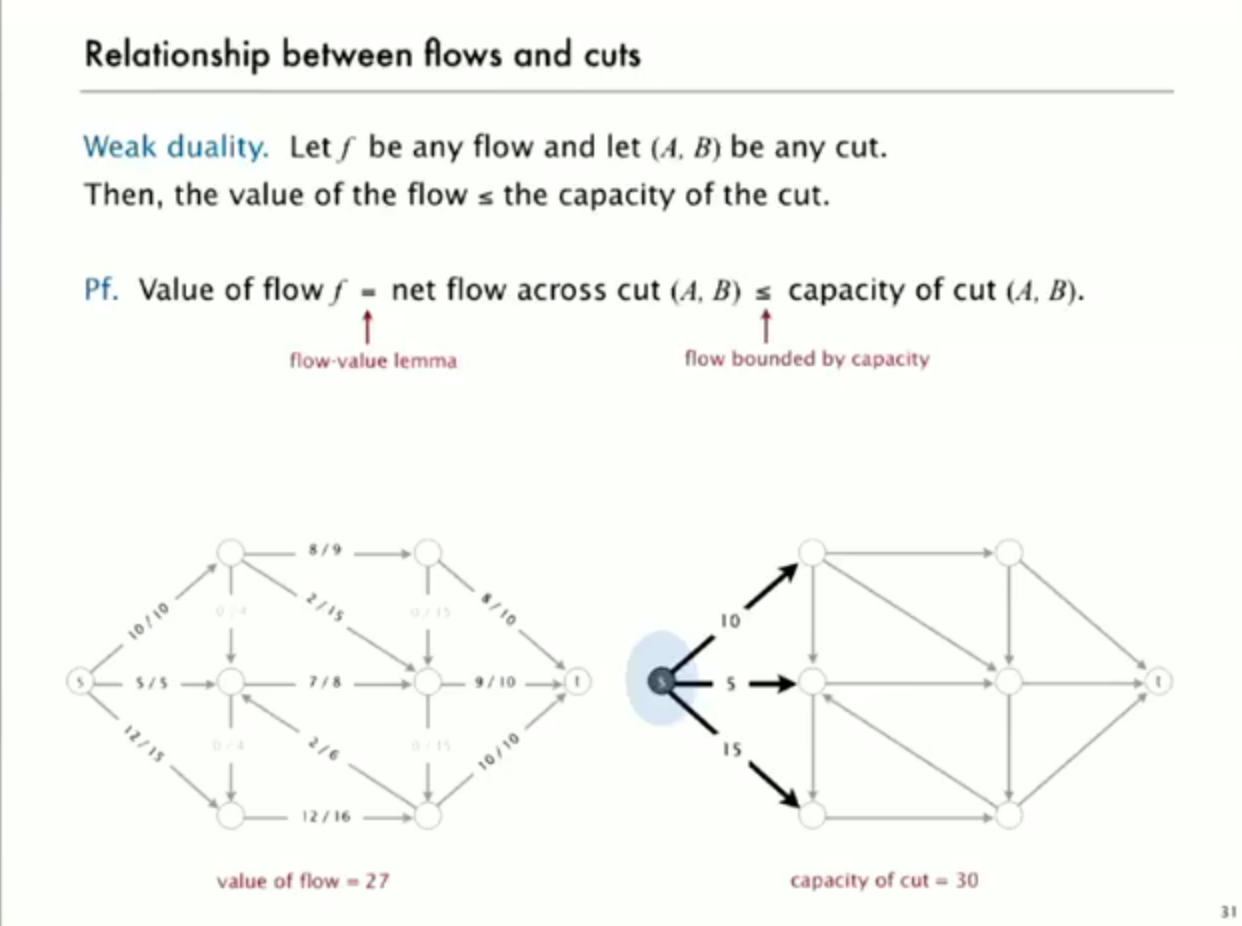
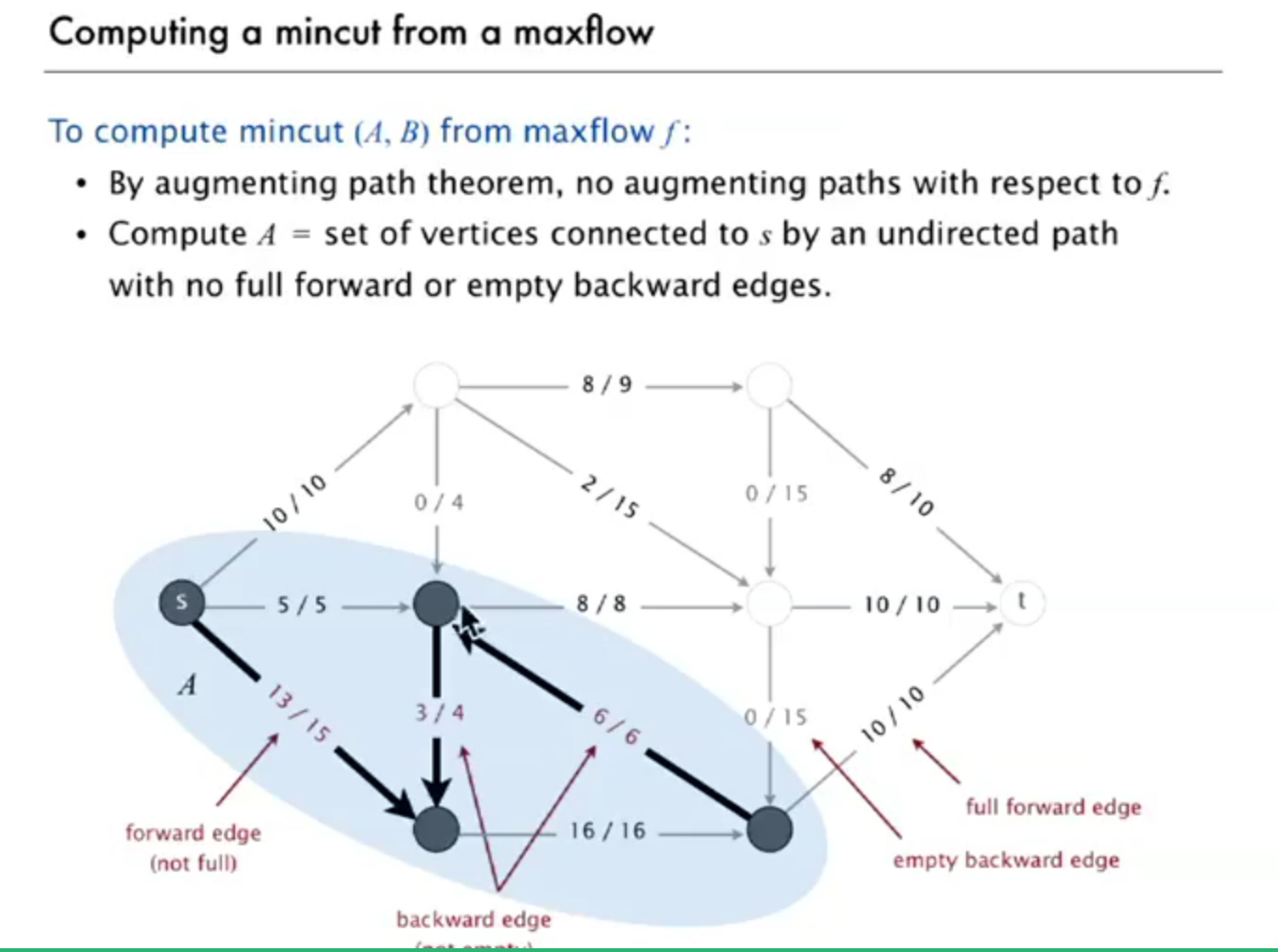
upload succeful

upload successl

upload successf

upload succsful

upload succeful

so how to find mincut from maxflow f?

start from s,find the forward edge that is not full or backward edge that is not empty

upload succesl

Ford-fulkerson算法

Ford-fulkerson算法就是： 不断在残留网络中找增广路，直到没有为止。

Time complexity : O(C*E) ,C 是容量和

1
Time complexity of the above algorithm is O(max_flow * E). We run a loop while there is an augmenting path. In worst case, we may add 1 unit flow in every iteration. Therefore the time complexity becomes O(max_flow * E).

Dinic 算法

Dinic: 每次寻找最短的增广路until找不到，可证明最多能找V次。

Time complexity : O（V^2E）

1
2
3
4
5
6
7
8
9
10
1) Initialize residual graph G as given graph.
1) Do BFS of G to construct a level graph (or
   assign levels to vertices) and also check if 
   more flow is possible.
    a) If more flow is not possible, then return.
    b) Send multiple flows in G using level graph 
       until blocking flow is reached. Here using 
       level graph means, in every flow,
       levels of path nodes should be 0, 1, 2...
       (in order) from s to t.

A flow is Blocking Flow if no more flow can be sent using level graph, i.e., no more s-t path exists such that path vertices have current levels 0, 1, 2… in order.

Dinic code-Kattis maximum flow

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
 #include <stdio.h>
#include <stdbool.h>
#include <bits/stdc++.h>
#define M 50
#define N 50
using namespace std;

//https://www.geeksforgeeks.org/dinics-algorithm-maximum-flow/


struct Edge {

    int to;
    unsigned long rev;//store index of reverse edge in adjacency
    int flow, cap;//cap is capacity
};

class Dinic {
    using AdjacencyList=vector< vector<Edge> >;

    bool bfs() {
        queue<int> q;
        q.push(source);
        fill(begin(levels), end(levels), -1);
        levels[source] = 0;
        while (!q.empty()) {
            const auto now = q.front(); q.pop();
            for (const auto& e : adjList[now]) {
                if (levels[e.to] == -1 && e.flow < e.cap) {
                    q.push(e.to);
                    levels[e.to] = levels[now] + 1;
                }
            }
        }
        return levels[sink] != -1;
    }

    //a dfs based function to send flow after BFS
//has figured out that there is a possible flow
//and constructed levels.This function called multiple times for a
//a single call of BFS
//flow: current flow sent by parent function call


    int dfs(int v, int flow) {
        if (flow == 0) return 0;
        if (v == sink) return flow;
        for (int & i = currentEdge[v]; i < (int) adjList[v].size(); ++i) {
            Edge& edge = adjList[v][i];
            if (levels[v] + 1 == levels[edge.to]) {
                const auto minimalFlow = dfs(edge.to, min(flow, edge.cap - edge.flow));
                if (minimalFlow > 0) {
                    //add flow to current edge
                    edge.flow += minimalFlow;
                    //subtract flow from reverse edge
                    adjList[edge.to][edge.rev].flow -= minimalFlow;
                    return minimalFlow;
                }
            }
        }
        return 0;
    }

    vector<int> levels, currentEdge;

public:

    int source, sink;
    AdjacencyList adjList;

    void AddEdge(int a, int b, int cap) {
        //ADJList动态变化，节省空间
        if (max(a, b) >= (int) adjList.size()) {
            adjList.resize(max(a, b) + 1);
            levels.resize(max(a, b) + 1);
            currentEdge.resize(max(a, b) + 1);
        }
        const auto rev_a = adjList[b].size();
        const auto rev_b = adjList[a].size();
        adjList[a].push_back({b, rev_a, 0, cap});
        adjList[b].push_back({a, rev_b, 0, 0});
    }

    int MaxFlow(int s, int t) {
        source = s;
        sink = t;
        int flow = 0;
        //augment the flow while there is path
        //from source to sink
        for (;;) {
            int m = bfs();
            if (!m) break;
            fill(begin(currentEdge), end(currentEdge), 0);
            while (int pushed = dfs(source, INT_MAX)) {
                flow += pushed;
            }
        }
        return flow;
    }

};

int main(){

    int n,m,s,t;
    cin>>n>>m>>s>>t;
    Dinic d;
    d.sink =s;
    d.source = t;
    vector<vector<int>>flow(n,vector<int>(n,0));
    for(int i=0;i<m;i++){
        int u,v,c;
        cin>>u>>v>>c;
        //flow[u][v] = c;
        d.AddEdge(u,v,c);
    }
    cout<<n<<" "<<d.MaxFlow(s,t)<<" ";
    //SIZE is the number of edges used in the solution
    //
    int size = 0;
    vector<tuple<int,int,int>>ans;
    for(int i=0;i<n;i++){
        for(auto &e:d.adjList[i]){
            if(e.flow>0)
            {
                size++;
                ans.push_back({i,e.to,e.flow});
            }
        }
    }
    cout<<size<<endl;
    for(auto &t:ans){
        int from = get<0>(t);
        int to = get<1>(t);
        int f = get<2>(t);
        cout<<from<<" "<<to<<" "<<f<<endl;
    }

}