CSAPP -Cache Lab

Part B

引用
https://blog.csdn.net/xbb224007/article/details/81103995?utm_source=blogxgwz0

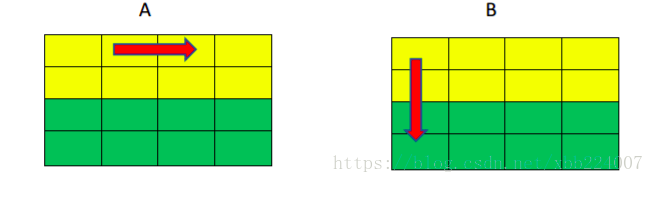
2-6就是常说的“抖动”

就是A，B数组下标相同的元素会映射到同一个cache块当中。

这里不命中本质上是因为访问同一个block的两个元素的时候，由于中间访问了其他块，导致已经加载的块被驱逐，进而导致第二次访问时候不命中。

解决办法： 同时把一个block若干个元素取出来，即省去了中间访问其他块导致驱逐的过程。利用blocking思想

CMU 文章
http://csapp.cs.cmu.edu/2e/waside/waside-blocking.pdf

1、A数组访问A[0][0]，冷不命中，将块11装入cache。

 2、B数组访问B[0][0]，虽然B[0][0]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache。

 3、A数组访问A[0][1]，虽然A[0][1] 所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。

 4、B数组访问B[1][0]，虽然B[1][0]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache。

 5、A数组访问A[0][2]，虽然A[0][2]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。

 6、B数组访问B[2][0]，B[2][0] 所映射的块12不在cache中，冷不命中，将数组B对应的块12装入cache。

 7、A数组访问A[0][3]，A[0][3]所映射的块11在cache中，且标记位相同，故命中。

 8、B数组访问B[3][0]，B[3][0]所映射的块12在cache中，且标记位相同，故命中。

 9、A数组访问A[1][0]，A[1][0]所映射的块11在cache中，且标记位相同，故命中。

 10、B数组访问B[0][1]，虽然B[0][1] 所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache。

 11、A数组访问A[1][1]，虽然A[1][1]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。

 12、B数组访问B[1][1]，虽然B[1][1]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组B对应的块11装入cache。

 13、A数组访问A[1][2]，虽然A[1][2]所映射的块11在cache中，但是标记位不同，造成冲突不命中，重新将数组A对应的块11装入cache。

 14、B数组访问B[2][1]，B[2][1] 所映射的块12在cache中，且标记位相同，故命中。

 15、A数组访问A[1][3]，A[1][3]所映射的块11在cache中，且标记位相同，故命中。

本实验的Cache

b = 5,s = 5，E=1

B =2^b = 2^5 = 32

S =2^s =2^5 =32

所以就是有32个块，每个块能存 32 bytes，就是8个int

先分析 32X32

一行32个元素，所以一行4个block，一共32个block，所以cache能应付8行。

所以每8行就会遇到冲突。就是两个int之间相差8行的整数倍，那么读取这两个元素所在的block就会发生替换

所以使用 8 * 8 blocking ，这样可以避免冲突

注意处理对角线的情况

因为矩阵转置之后，A【i,j】 = B【j,i】是相等的。

所以会发生冲突，可以采取的方法是，遇到对角线上的元素先不放到B，等block的其他七个元素写完之后，再把这个元素写到目的地。避免了由于中间加载B块，导致A块被驱逐所引起的命中冲突。

代码：

if(M==32)
{   //separate the the 32X32 block into 8X8 , decrease the number of misses
    for(row_Block = 0;row_Block < N ;row_Block+=8){
        for(col_Block =0 ;col_Block < M; col_Block+=8){
            for(i=row_Block ; i<row_Block+8;i++){
                for(j=col_Block;j<col_Block+8;j++){
                    if(i!=j){
                        B[j][i] = A[i][j];
                    }else{
                        tmp = A[i][j];                  //i==j means is the diagonal. if we set B right now ,the  misses and evictions will increase . because the cache set of B is same to A.
                        index = i;
                    }
                }
                if(col_Block == row_Block){             //just set B on the diagonal. other than shouldn't set the B
                    B[index][index] = tmp;
                }
            }
        }
    }
}

分析 61 x 67 情况

尝试 88,1616,17*17等各种情况即可。

最难的就是

64 X 64 情况

一行用掉8个block，所以每4行就会发生冲突。

1.先要想清楚，转置的时候，对A数组是按行访问的，而对与B数组是按列访问的。

我们先来分析一下，如果在64 x 64情况下 ，采用8分块，那列访问B的时候，前四行和后四行映射的块是相同的。

所以会发生这种情况：

1.访问前4行第一列之后，再访问后4行的第一列，会发生冲突，使得原来的块被驱逐。

2.再回去访问前四行的第二列，由于原来的块被驱逐，又会导致冲突不命中，

3.访问后4行第二列又产生冲突不命中。

如果采用 4 X 4 分块

对于B 数组而言，访问顺序为
前四行前四列-》后四行前四列-》前四行后四列-》后四行后四列

这里有点不懂

参考文章提到，后四行前四列所在的块会覆盖前四行前四列的块，后面两次访问又会有一次不命中。为什么是2次？不是3次？

因此采取的策略：

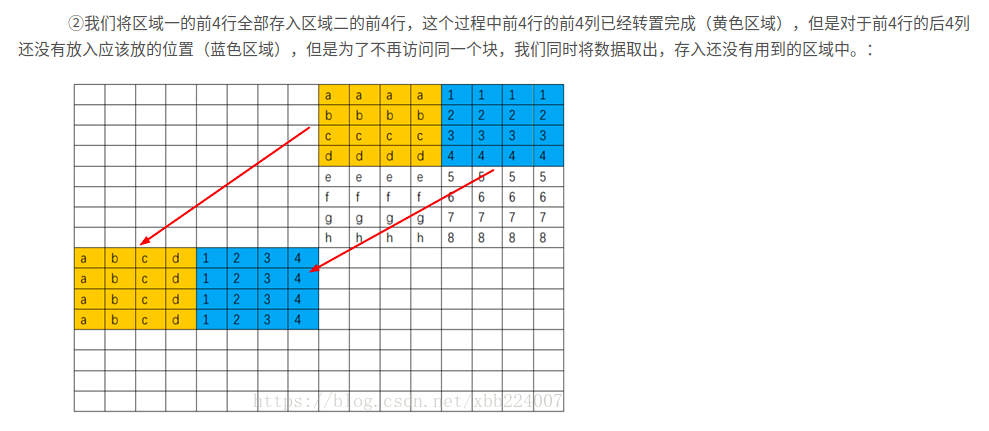
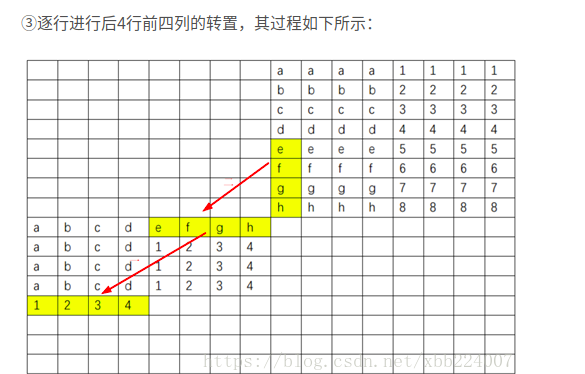
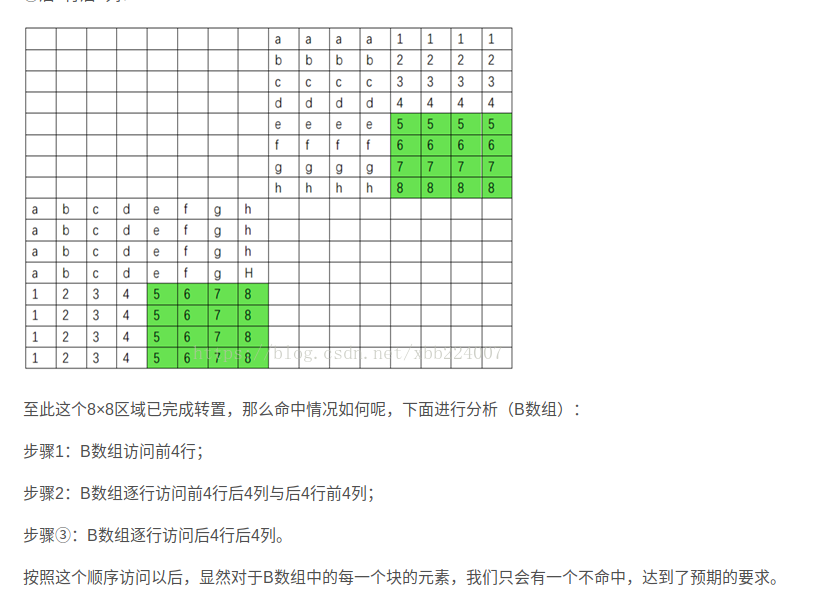
按照这个顺序，对于B数组每一个块的元素，只会有一次不命中

else if(M==64){
     for (i = 0; i < N; i+=8) {
         for (j = 0; j < M; j+=8) {
             for(x=i;x<i+4;x++){

                 x1 = A[x][j];
                 x2 = A[x][j+1];
                 x3 = A[x][j+2];
                 x4 = A[x][j+3];
                 x5 = A[x][j+4];
                 x6 = A[x][j+5];
                 x7 = A[x][j+6];
                 x8 = A[x][j+7];
                 //leftup as usual
                 B[j][x] = x1;
                 B[j+1][x] = x2;
                 B[j+2][x] = x3;
                 B[j+3][x] = x4;
                 B[j][x+4] = x5;
                 B[j+1][x+4] = x6;
                 B[j+2][x+4] = x7;
                 B[j+3][x+4] = x8;
             }
             for(y=j;y<j+4;y++){
                 
                 x1 = A[i+4][y];
                 x2 = A[i+5][y];
                 x3 = A[i+6][y];
                 x4 = A[i+7][y];
                 x5 = B[y][i+4];
                 x6 = B[y][i+5];
                 x7 = B[y][i+6];
                 x8 = B[y][i+7];

                 B[y][i+4] = x1;
                 B[y][i+5] = x2;
                 B[y][i+6] = x3;
                 B[y][i+7] = x4;
                 B[y+4][i] = x5; 
                 B[y+4][i+1] = x6;
                 B[y+4][i+2] = x7;
                 B[y+4][i+3] = x8;
             }

             for(x = i+4;x<i+8;x++){
                 x1 = A[x][j+4];
                 x2 = A[x][j+5];
                 x3 = A[x][j+6];
                 x4 = A[x][j+7];

                 B[j+4][x] = x1;
                 B[j+5][x] = x2;
                 B[j+6][x] = x3;
                 B[j+7][x] = x4;

             }
         }
     }
 }

上述代码就是：

1. B数组访问前4行

2. B数组访问前四行后四列，和后四行前四列

3. B数组最后把后四行后四列转置

我感觉就是先把一行的数据处理完再去处理下一行，尽量不要交替着4行访问数据，这样会导致块被驱逐，加载，增加了总的冲突次数。